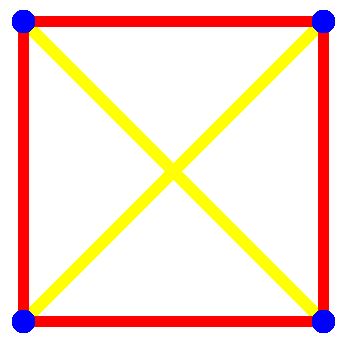
Alex Bellos set a pleasingly simple puzzle in Monday’s Guardian: How many ways are there to arrange four points in the plane so that only two distances occur between any two points? He gives one solution, which helps to illustrate the problem: In a square, any two vertices are separated by either the length of a side or the length of a diagonal — no matter which two points are chosen, the distance between them will be one of two values. Besides the square, how many other configurations have this property?
The puzzle comes originally from Dartmouth mathematician Peter Winkler, who writes, “Nearly everyone misses at least one [solution], and for each possible solution, it’s been missed by at least one person.”
