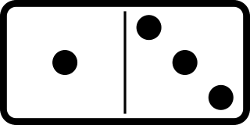
A problem proposed by C. Gebhardt in the Fall 1966 issue of Pi Mu Epsilon Journal:
A particular set of dominoes has 21 tiles: (1, 1), (1, 2), … (1, 6), (2, 2), … (6,6). Is it possible to lay all 21 tiles in a line so that each adjacent pair of tile ends matches (that is, each 1 abuts a 1, and so on)?
|
SelectClick for Answer |
Solution by Craig A. Kalicki of John Carroll University:
Because like numbers must abut, each number must appear an even number of times in the interior of the chain. But the set contains seven instances of each number. Hence if the task is to be completed, each of the six numbers must make an appearance at one of the chain’s ends. The chain has only two ends, so the task is impossible.
(“Problem Department,” Pi Mu Epsilon 4:5 [Fall 1966], 205-210.)
|

