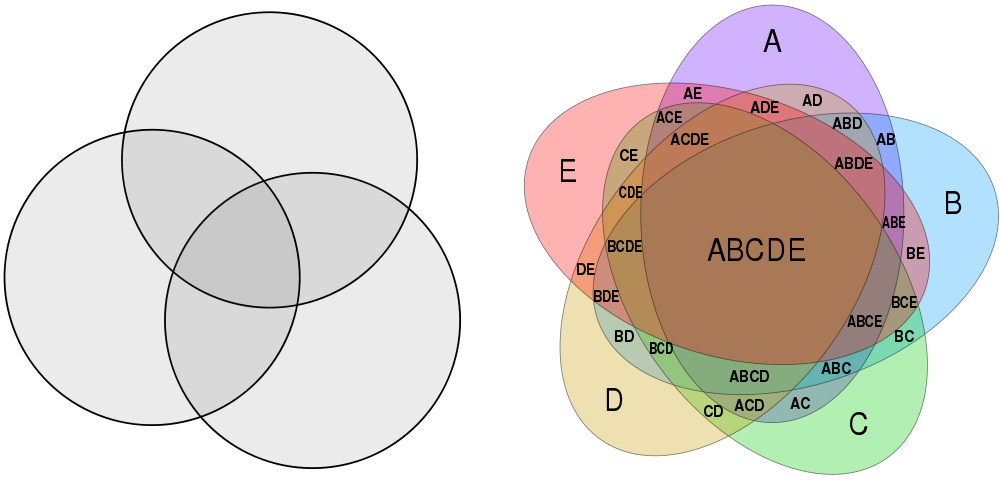
The classic three-circle Venn diagram on the left has threefold rotational symmetry, and the more complex five-ellipse diagram on the right (discovered by Branko Grünbaum in 1975) has fivefold symmetry. Pleasingly, it turns out that a Venn diagram with n curves having an n-fold rotational symmetry exists if and only if n is prime.

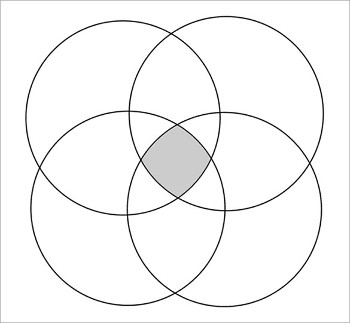
(The diagram below has four curves and fourfold symmetry, but properly speaking it’s not a Venn diagram because it doesn’t represent all possible intersections of the sets.)

(Stan Wagon and Peter Webb, “Venn Symmetry and Prime Numbers: A Seductive Proof Revisited,” American Mathematical Monthly 115:7 [2008], 645-648; Frank Ruskey, Carla D. Savage, and Stan Wagon, “The Search for Simple Symmetric Venn Diagrams,” Notices of the AMS 53:11 [2006], 1304-1311.)