Quickie - Futility Closet

Quickie

If I roll three dice and multiply the three resulting numbers together, what is the probability that the product will be odd?

	Select Click for Answer
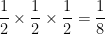
The product can be odd only if all three factors are odd: $\displaystyle \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{8}$ (Thanks, Nick.) 02/01/2021 UPDATE: From reader Paul-Georg Becker: Another dice quickie: I have a set of n dice, but unfortunately only one of them is fair. If I roll all dice and add the n resulting numbers together, what is the probability that the product will be odd? Answer: For natural n let S_n be the sum of the resulting numbers x₁, …, x_n. We assume that x_n is the number shown by the fair die. Then we have P(S_n even) = P(x_n + S_n-1 even) = P(S_n-1 even) P(x_n even) + P(S_n-1 odd) P(x_n odd) = P(S_n-1 even) /2 + P(S_n-1 odd) / 2 = (P(S_n-1 even) + P(S_n-1 odd)) / 2 = 1/2 It does not even matter what the result for S_n-1 is. (Thanks, Paul-Georg.)