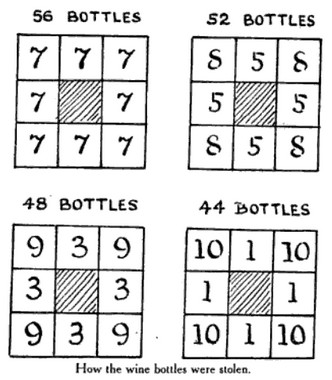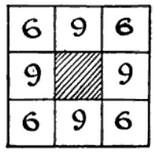
A puzzle by Claude Gaspar Bachet de Méziriac, from 1612, via Henry Dudeney:

A gentleman had a wine-bin of eight compartments, as in the illustration, containing 60 bottles, arranged as shown. His dishonest servant stole 4 bottles and rearranged the remainder. The gentleman noticed that the bottles had been redistributed, but as there were still 21 bottles on every side he innocently concluded that all the 60 were there. The servant, emboldened by his success, again stole 4 bottles and rearranged the remainder without discovery. In fact, on two more occasions he repeated his theft of 4 bottles, always leaving the remainder so arranged symmetrically that there were 21 on every side. How did he arrange them on the four occasions so as to steal the 16 bottles?