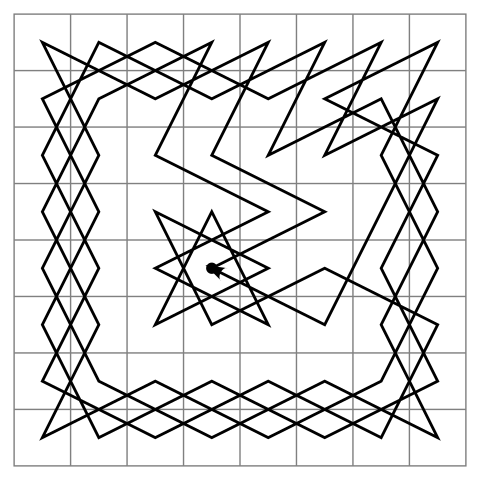
A knight’s tour is a series of moves by a chess knight such that it visits each square on the chessboard once. The example above is a “closed” tour because it ends on the square where it started.

This inspired a puzzle posed by Martin Gardner. If we filled a standard chessboard with knights, one on each square, could all 64 of them move simultaneously? The closed knight’s tour shows that they could — they form a long conga line, with each knight vacating a square for the knight behind it to occupy.

Gardner asks: Could the same feat be accomplished on a 5 × 5 chessboard?