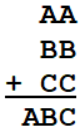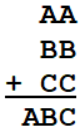A puzzle from reader Steven Moore:
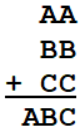
Find A, B, and C as distinct integers. There is only one solution.
|
SelectClick for Answer |
- The maximum value of ABC is 99 + 88 + 77 = 264. Therefore, A can only be 1 or 2.
- Looking at the 1s column, A + B must add to 10 because C appears in the 1s place of the sum as well as in the 1s place in one of the addends.
- Since A can be only 1 or 2, B can be only 9 or 8.
- Now we have only the following two possibilities:
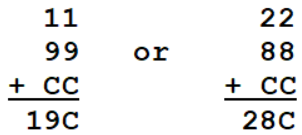
- 28C is going to be larger than the maximum value of 264. Therefore 11 + 99 + CC = 19C and C can only be 8.
- A = 1, B = 9, C = 8.
(Thanks, Steven.)
|