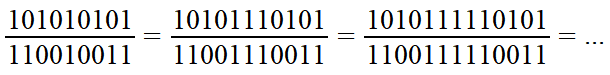
P. Anning noted this curiosity in Scripta Mathematica in 1956 — if the middle digit 1 in both the numerator and denominator of 101010101/110010011 is replaced with any odd number of 1s, then the proportion remains the same. And all of these numbers are palindromes!

Waclaw Sierpinski gives a proof in 250 Problems in Elementary Number Theory (1970).