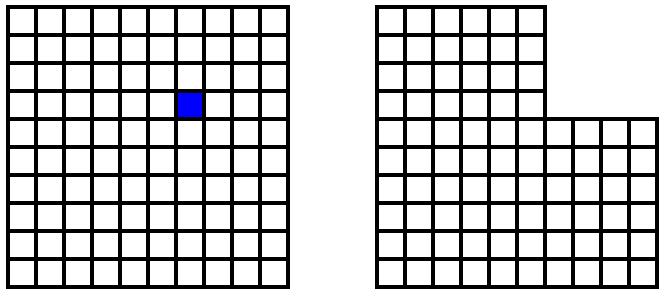
In the game Chomp, two players begin with a rectangular grid. The first player chooses any square and removes it from the grid, together with all the squares above and to the right of it. The second player chooses one of the remaining squares and removes that, together with all the squares above it and to its right. The two take turns in this way until one of them is forced to remove the last square. That player loses.
If the starting grid is square, can either player force a win?
|
SelectClick for Answer |
The first player can force a win by choosing the square immediately northeast of the lower left corner square:
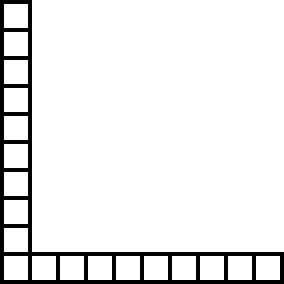
This reduces the grid to a big L. Now the first player simply aims for symmetry: If the second player removes three squares from one leg of the L, the first removes three squares from the other. Eventually the second player will be forced to take the last square and lose the game.
From Paul Halmos, Problems for Mathematicians, Young and Old, 1991. Similar: Breaking Bad.
|


