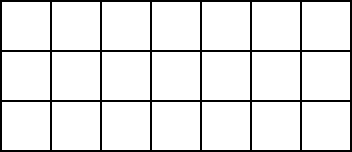
“Here is an old favorite of mine that completely stumped me once when I was a student,” writes Jeff Hooper in Crux Mathematicorum. Suppose that each square in this 3×7 grid is painted red or black at random. Show that the board must contain a rectangle whose four corner squares are all the same color.
|
SelectClick for Answer |
Each column contains 3 squares, so each of the 7 columns must contain 2 squares of the same color. There are 3 ways to position 2 black squares in a column, and 3 ways to position 2 red squares, for 6 possibilities overall. Since there are 7 columns in the grid, some 2 of them must bear the same pattern, and thus there are 2 different columns that each contain 2 squares with the same color and position. These form the corners of a rectangle.
(Jeff Hooper, “Pólya’s Paragon,” Crux Mathematicorum 33:3 [March 2007], 146-148.)
|

