Two runners start from the same point on a circular track and run at different constant speeds. If they run in opposite directions on the track, they meet after a minute. If they run in the same direction, they meet after an hour. What’s the ratio of their speeds?
|
SelectClick for Answer |
Dartmouth mathematician Peter Winkler writes, “This is simultaneously confusing and easy.” Let L be the length of the track. Now, when the two runners are going in opposite directions, they’ll meet when they’ve covered a combined distance L. When they’re going in the same direction, they’ll meet when the difference between the distances they’ve covered is L. So
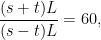
and we find that s/t = 61/59.
From Dick Hess, Golf on the Moon, 2014, via Winkler’s excellent collection Mathematical Puzzles, 2021.
|
