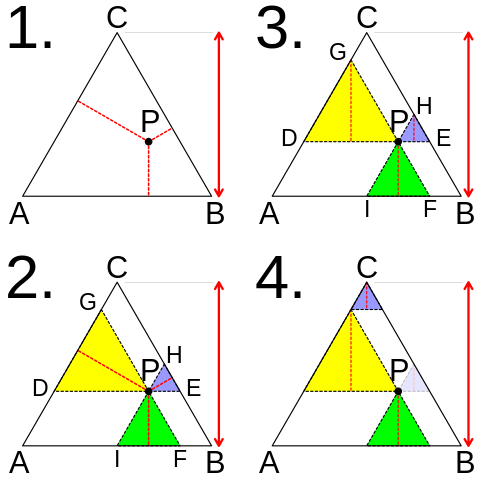
Pick any point in the interior of an equilateral triangle and draw a perpendicular to each of the three sides. The sum of these perpendiculars is the height of the triangle.

That’s Viviani’s theorem. This visual proof is by CMG Lee:

1. Choose point P and draw the three perpendiculars.
2. Now draw three lines through P, each parallel to a side of the main triangle. This creates three small similar triangles.
3. Because these smaller triangles are equilateral, we can rotate each so that its altitude is vertical.
4. Because PGCH is a parallelogram, we can slide triangle PHE to the top, and now the heights of the three constituent triangles sum to that of triangle ABC.

The converse of the theorem is also true: If the sum of the perpendiculars from a point inside a triangle to its sides is independent of the point’s location, then the triangle is equilateral.