Suppose we drop a glass rod and it breaks into three pieces. What is the probability that the pieces can form a triangle? Mathematician D.C. Johnson found this elegant geometric solution. In order to form a triangle, none of the three pieces can be longer than the other two combined. Now consider an equilateral triangle whose altitude equals the length of the glass rod (say, 1). Viviani’s theorem tells us that the sum of the lengths of the perpendiculars from any interior point to the sides of this triangle is 1, the triangle’s altitude:

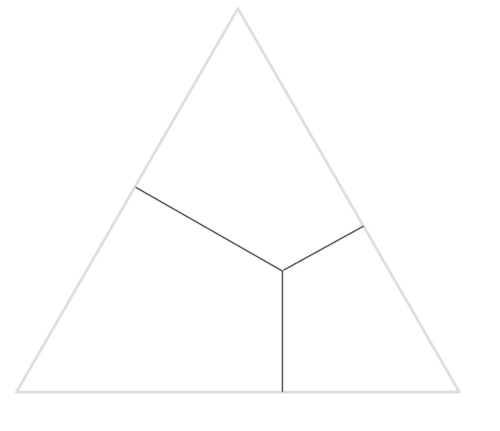
And any three non-negative numbers whose sum is 1 correspond to three such perpendiculars in some prescribed order. So the points inside the triangle correspond to all the various ways in which the glass rod can break.

Now consider the first piece of the broken rod. In order to form a triangle with the other two pieces, its length must not exceed 1/2. That means it must not extend from the base of our equilateral triangle into the shaded zone here:

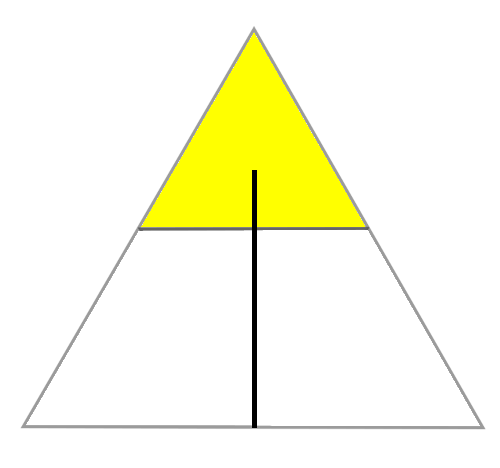
And if we assign the other two pieces to the other two legs, we can make the same argument and identify two more zones:

That immediately gives the answer: The chance that all three pieces will be short enough to produce a triangle is 1 in 4.

(C. Haigh, “The Glass Rod Problem,” Mathematical Gazette 65:431 [March 1981], 37-38.)