A Pi Diet

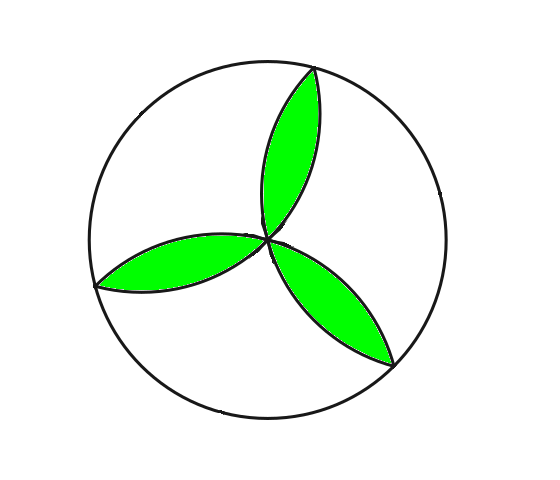
https://commons.wikimedia.org/wiki/File:Academ_rosette.svg Image: <a href="https://commons.wikimedia.org/wiki/File:Academ_rosette.svg">Wikimedia Commons</a>

Students beginning with the compass learn to draw this rosette, sometimes called the Flower of Life. If the arcs and the circle have the same radius, a, then the area of one petal is

\displaystyle X = a^{2}\left ( \frac{\pi }{3} - sin \frac{\pi }{3}\right ) = \left ( \frac{\pi }{3} - \frac{\sqrt{3}}{2}\right ) a^{2}

and the unshaded area of the circle is

\displaystyle Y = \pi a^{2} - 3X = \frac{3\sqrt{3}}{2}a^{2}.

Remarkably, though the area we sought is bounded entirely by the arcs of circles, the final expression is independent of π.

Related: When two cylinders of radius r meet at right angles, the volume of their intersection is 16r3/3 — again, no sign of π.

(J.V. Narlikar, “A Pi-Less Area,” Mathematical Gazette 65:431 [March 1981], 32-33.)

10/01/2024 UPDATE: Some deft rearranging shows that the unshaded area of the circle is just the area of an inscribed regular hexagon:

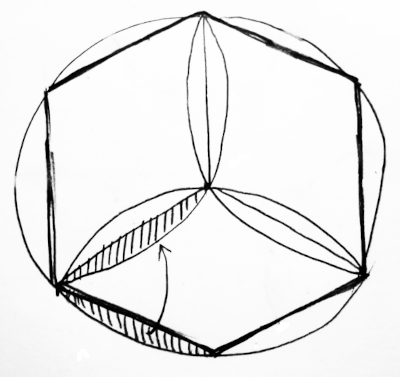
2024-09-28-a-pi-diet-2

So the absence of π isn’t that surprising. Thanks to readers Catalin Voinescu (who sent this diagram) and Gareth McCaughan for pointing this out.

| Science & Math