An art gallery with n walls will always be safe with n/3 guards — the guards will always be able arrange themselves to observe the whole gallery.

That’s Chvátal’s art gallery theorem, discovered in 1973 by mathematician Václav Chvátal. Interestingly, it’s true only of two-dimensional floor plans — a three-dimensional gallery may not be safe even if you post a guard at every corner.

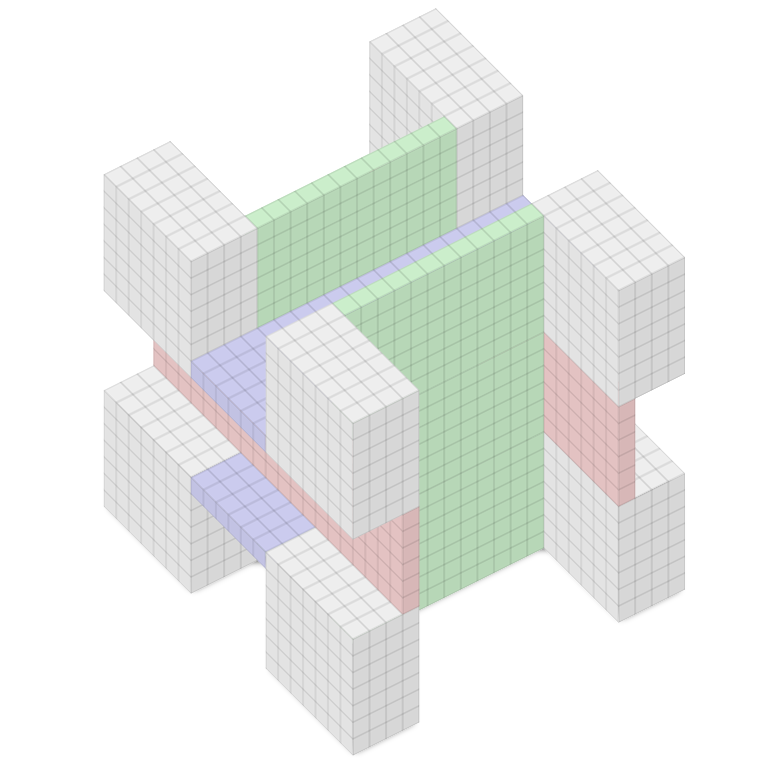
Take a 20 × 20 × 20 cube and remove a 12 × 6 channel from the front and back faces; a 6 × 3 channel from the left and right faces; and a 6 × 6 channel from the top and bottom faces, as shown. The result is the Octoplex, eight 4 × 7 × 7 theaters connected to each other and to a central lobby by passages 1 unit wide.

Remarkably, even if we mount a camera at every one of this figure’s 56 corners, there will remain a small region in the central lobby that no camera can see.

(T.S. Michael, “Guards, Galleries, Fortresses, and the Octoplex,” College Mathematics Journal 42:3 [May 2011], 191-200.)