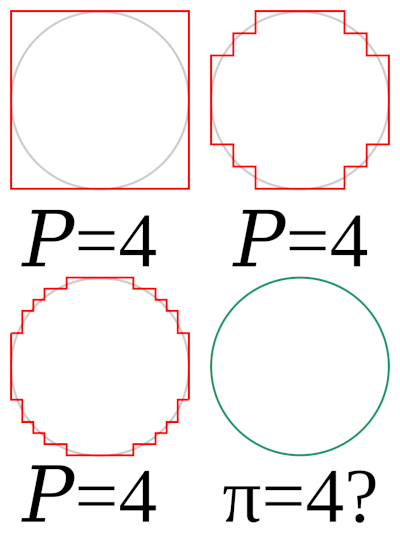
Uh-Oh


London doctor Thomas Ellerby had strong feelings about the disposal of his remains — in his will of February 1827 he threatens to haunt his doctors if they don’t follow his instructions:
I bequeath my heart to Mr. W., anatomist; my lungs to Mr. R.; and my brains to Mr. F., in order that they may preserve them from decomposition; and I declare that if these gentlemen shall fail faithfully to execute these my last wishes in this respect I will come — if it should be by any means possible — and torment them until they shall comply.
The Lancet records that “[t]he gentlemen named — eminent in their day — rightly renounced the legacies left them, and it never appeared that they were, like St. Dunstan and other medieval saints, tromented by visitations from the other world.”

George Sicherman, of Sicherman dice fame, has designed a puzzle to welcome the new year: Print out the PDF, cut out the letters MMXXVI (the Roman numerals for 2026), and fit them into the tray provided so that no pieces with the same shape touch one another.
Sicherman’s website has a whole range of puzzles, most of them geometric.
(Thanks, William.)
In November 1943, as they planned a summit meeting, FDR wired Churchill to suggest that Cairo might be too dangerous a location. Churchill responded:
SEE ST. JOHN, CHAPTER 14, VERSES 1 TO 4.
These verses read:
They met in Cairo.
Does the sequence of squares contain an infinite arithmetic subsequence?
In 1582, as the Catholic world prepared to adopt the new Gregorian calendar, German pamphleteers lampooned the strife that attended the change:
The old calendar must be the right one for the animals still use it. The stork flies away according to it, the bear comes out of his hole on the Candlemas day of the old calendar and not of the Pope’s, and the cattle stand up in their stalls to honor the birth of the Lord on the Christmas night of the old and not of the new calendar. They also recognize in this work diabolical wickedness. The Pope was afraid the last day would come too quickly. He has made his new calendar so that Christ will get confused and not know when to come for the last judgment, and the Pope will be able to continue his knavery still longer. May Gott him punish.
“Inanimate objects were not so stubborn.” An Italian walnut tree that had reliably put forth leaves, nuts, and blossoms on the night before Saint John’s day under the old regime dutifully adopted the new calendar and performed its feat on the correct day in 1583. A traveler wrote, “I have today sent a branch, broken off on Saint John’s day, to Herr von Dietrichstein, who no doubt will show it to the Kaiser.”
(Roscoe Lamont, “The Reform of the Julian Calendar,” Popular Astronomy 28:1 [January 1920], 18-32.)
The Universe and the Philosopher sat and looked at each other satirically. …
‘You know so many things about me that aren’t true!’ said the Universe to the Philosopher.
‘There are so many things about you that you seem to be unconscious of,’ said the Philosopher to the Universe.
* * *
‘I contain a number of things that I am trying to forget,’ said the Universe.
‘Such as what?’ asked the Philosopher.
‘Such as Philosophers,’ said the Universe.
‘You are wrong,’ said the Philosopher to the Universe, ‘for it is only by working up the most important part of yourself into the form of Philosophers that you get a product capable of understanding you at all.’
‘Suppose,’ said the Universe, ‘that I don’t care about being understood. Suppose that I care more about being?’
‘You are wrong again, then,’ said the Philosopher. ‘For being that is not conscious being can scarcely be called being at all.’
***
‘You Philosophers always were able to get the better of me in argument,’ smiled the Universe, ‘and I think that is one thing that is the matter with you.’
‘If you object to our intellects,’ said the Philosopher, ‘we can only reply that we got them, as well as everything else, from you.’
‘That should make you more humble,’ said the Universe. ‘If I quit letting you have intellect, where would you be then?’
‘Where would you be,’ asked the Philosopher, ‘if you quit letting me have intellect? If I quit thinking you out as you are, and must be, you would cease to exist as you are; for I am a part of you; and if I were to change, your total effect would be changed also.’ … Then the Philosopher reflected a long moment, and, warming to his work, put over this one: ‘The greater part of you, for all I know, exists in my brain anyhow; and if I should cease to think of that part, that part would cease to be.’
* * *
‘You make me feel so helpless, somehow!’ complained the Universe, hypocritically. ‘I beg your pardon for asking you to be humble a moment ago. … I see now, very plainly, that it is I who should be more humble in your presence.’
‘I am glad,’ said the Philosopher, ‘that we have been able to arrive at something like an understanding.’
‘Understanding!’ echoed the Universe. ‘It’s so important, isn’t it?’ … And then: ‘Come! We have argued enough for one day! There is something terribly fatiguing to me about Profound Thought. Can’t we just lie down in the shade the rest of the afternoon and watch the wheels go round?’
‘Watch the wheels go round?’ puzzled the Philosopher.
‘Uh-huh ! … the planets and solar systems, and stuff like that. The nicest thing in life, as I have lived it, is just to lie about and drowse and watch the wheels go round. … I made nearly everything spherical in the beginning so it would roll when I kicked it. I’d rather play than think.’
‘You are a Low Brow!’ said the Philosopher.
‘Uh-huh,’ said the Universe. ‘At times. … I suppose that’s the reason some of the children neglect the old parent these days.’
* * *
And then, after a nap, during which the Philosopher contemplated the Universe with a tinge of superiority, the Universe rumbled sleepily: ‘I know what I am going to do with this Intellect Stuff. I’m going to take it away from you Philosophers and give it to fish or trees or something of that sort!’
‘How frightfully grotesque!’ said the Philosopher, turning pale.
‘Or to giraffes,’ continued the Universe. ‘Giraffes are naturally dignified. And they aren’t meddlesome. I’d like to see a whole thousand of giraffes walking along in a row, with their heads in the air, thinking, thinking, thinking … with tail coats and horn-rimmed goggles.’
* * *
‘You are absurd!’ cried the Philosopher.
‘Uh-huh,’ said the Universe. And reaching over, the Universe picked up the Philosopher, not ungently, by the scruff of the neck, tossed him into the air, caught him tenderly as he came down, spun him around, and set him right side up on the ground.
‘You,’ said the Universe, grinning at the breathless Philosopher pleasantly, ‘are sort of funny yourself, sometimes!’
The index to David Lloyd George’s 1938 War Memoirs sums up his feelings about Field Marshal Douglas Haig:
his refusal to face unpleasant facts
his limited vision
Germans accustomed to his heavy-footed movements
his stubborn mind transfixed on Somme
his misconceptions concerning morale of German army
obsessed with Passchendaele and optimistic as to military outlook
none of his essential conditions for success prevail at Passchendaele
misrepresents French attitude
his plans strongly condemned by Foch
misleads Cabinet about Italian Front
prefers to gamble his hopes on men’s lives than to admit an error
completely ignorant of state of ground at Passchendaele
fails to appreciate the value of tanks
not anxious for success on Italian Front
a mere name to men in the trenches
narrowness of his outlook
incapable of changing his plans
his judgement on general situation warped by his immediate interests
his fanciful estimates of man-power
jealous of Foch
does not expect big German attack in 1918
distributes his reserves very unwisely
his conduct towards Fifth Army not strictly honourable
his unwise staff appointments
his defeatist memorandum of 25/3/18
unfairly removes Gough from command of Fifth Army
his complaints as to lack of men unjustified
does not envisage Americans being of use in 1918
stubbornness
unreliability of his judgments
launches successful attack of 8/8/18 […] but fails to follow it up
his censorious criticism of his associates
his attempt to shirk blame for March, 1918, defeat
only took part in one battle during War
Also: “unequal to his task”, “industrious but uninspired”, “did not inspire his men”, “entirely dependent on others for essential information”, “the two documents that prove his incapacity”, “unselfish but self-centred”, “his inability to judge men”, “liked his associates to be silent and gentlemanly”, “his contempt for Foch”, “his intrigues against Lord French and Kitchener”, “his failure at Loos”, “his ingenuity in shifting blame to other shoulders than his own”, “his shabby treatment of Gough”, and “his conspiracy to destroy General Reserve”. He found in Haig’s diaries “a sustained egoism which is almost a disease.”
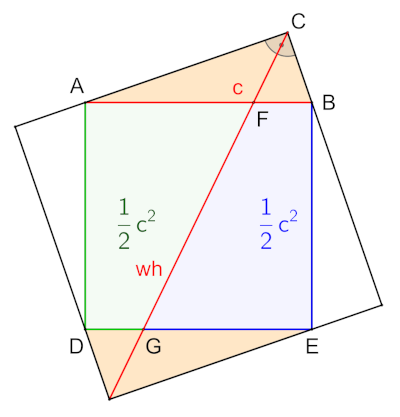
In any right triangle, the angle bisector of the right angle divides the square on the hypotenuse into two congruent trapezoids.
fIVe + sIX + seVen
5 + 6 + 7 = 18
IV + IX + V = 18
These are the only three consecutive numbers whose sum equals that of the Roman numerals embedded in their names.