Author: Greg Ross
Points of Pride
She’s the girl that makes the thing that drills the hole that holds the spring
That drives the rod that turns the knob that works the thingumebob,
And it’s the girl that makes the thing that holds that oil that oils the ring
That works the thingumebob THAT’S GOING TO WIN THE WAR!
“I’ve Danced With a Man, Who’s Danced With a Girl, Who’s Danced With the Prince of Wales”
Dr. Polycarp was, as you all know, an unusually sallow bimetallist. ‘There,’ people of wide experience would say, ‘There goes the sallowest bimetallist in Cheshire.’
— G.K. Chesterton, The Napoleon of Notting Hill, 1904
“Hallelujah!”
“Hallelujah!” was the only observation
That escaped Lieutenant-Colonel Mary Jane,
When she tumbled off the platform in the station,
And was cut in little pieces by the train.
Mary Jane, the train is through yer:
Hallelujah, Hallelujah!
We will gather up the fragments that remain.
— A.E. Housman
Query
From Gerald Lynton Kaufman’s The Book of Modern Puzzles (1954):
- All DROONS are the same size and shape.
- All green SLACKENS are the same size and shape.
- Twenty DROONS just fill up a MULDRUFF.
- All WALLAXES contain green SLACKENS.
- A green SLACKEN is 10% bigger than a DROON.
- A WALLAX is smaller than a MULDRUFF.
“If all MULDRUFFS and all WALLAXES are predominantly RED throughout, what is the largest possible number of green SLACKENS in a WALLAX?”
Impostor

Visiting Hamburg in 1878, Mark Twain heard a cuckoo calling in the woods.
“First cuckoo I ever heard outside of a clock,” he wrote. “Was surprised how closely it imitated the clock — and yet of course it could never have heard a clock.”
He added, “The hatefulest thing in the world is a cuckoo clock.”
(From his Notebook.)
Nobility

English essayist Henry W. Nevinson defined chivalry as “going about releasing beautiful maidens from other men’s castles, and taking them to your own castle.”
Dead Letters
In 1814, as the British burned Washington, commander Sir George Cockburn targeted the offices of the National Intelligencer newspaper, telling his troops, “Be sure that all the C’s are destroyed, so that the rascals cannot any longer abuse my name.”
British politician Thomas Erskine (1750-1823) had such an enormous ego that, it was said, one newspaper had to curtail its coverage because its “stock of capital I’s was quite exhausted.”
Roundabout
Alsatian pastor J.G. Stuber composed this puzzle canon in the late 18th century.
“It was always a great delight to me, in riding my horse from one village to another, to hear in the fields and among the heights the melodies which I had taught,” he wrote. “I could often distinguish very beautiful and harmonious voices.”
Home Again
As Governor of Mauritius, [Theodore] Hook ruled for five years before being accused of embezzling 12,000 pounds of public funds. He was dismissed from his post and returned to England, where he told friends that his dismissal was ‘on account of a disorder in my chest.’
— Victor Margolin, “The Pun Is Mightier Than the Sword: A Short History of Paronomasia,” Verbatim, Summer 1980
All the Way Down

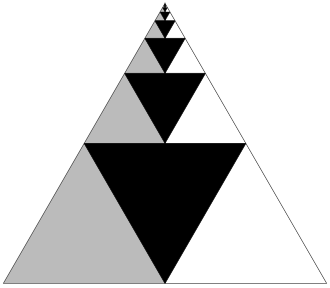
The infinite series 1/4 + 1/16 + 1/64 + 1/256 + … was one of the first to be summed in the history of mathematics; Archimedes had found by 200 BC that it totals 1/3. There are two neat visual demonstrations that make this fact immediately apparent. In the unit square above, the largest black square has area 1/4, the next-largest black square has area 1/16, and so on. Regions of black, white, and gray make up equal areas in the total figure, so the black squares, taken together, must have area 1/3.
The same argument can be made using triangles (below). If the area of the largest triangle is 1, then the largest black triangle has area 1/4, the next-largest 1/16, and so on. Areas of black, white, and gray make up equal parts of the total figure, so the black regions must total 1/3.