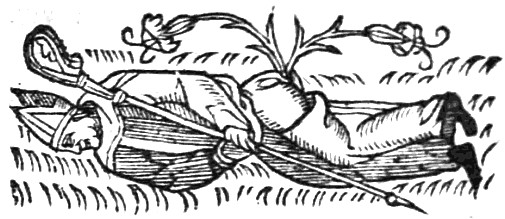
At Nuremburg a wolf’s tooth was shown to travellers … on which an Abbé is represented lying dead in a meadow, with three lilies growing out of his posteriors. This is not only the worst pun that ever was carved upon a wolf’s tooth, but the worst that ever was or will be made. The Abbé is designed to express the Latin word Habe. He is lying dead in a meadow, … mort en pré; this is for mortem præ; and the three lilies in his posteriors are to be read oculis, … au cu lis. Thus, according to the annexed explanation, the whole pun, rebus, or hieroglyphic, is Habe mortem præ oculis.
— Robert Southey, Omniana, 1812
In other words, the French phrase Abbé mort en pré au cul lys (“Abbot died in a meadow with lilies in his rump”) sounds like the Latin phrase Habe mortem præ oculis (“Keep death before your eyes”). This joke appears to be referenced in Hieronymus Bosch’s 1504 triptych The Garden of Earthly Delights: