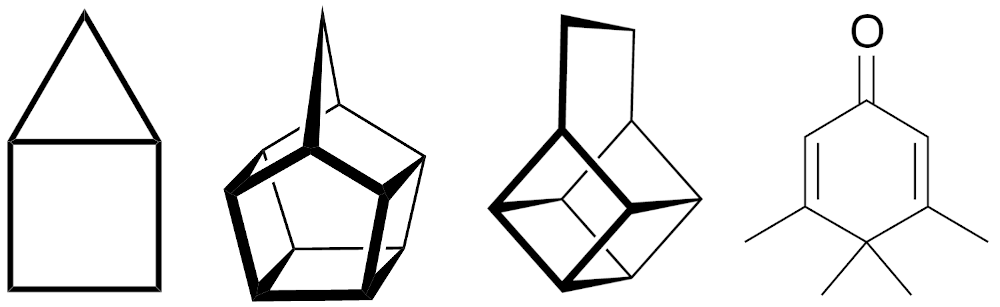
These compounds are named housane, churchane, basketane, and penguinone.
Below: To celebrate the 2012 London Olympics, chemists Graham Richards and Antony Williams offered a molecule of five rings. They called it olympicene.

These compounds are named housane, churchane, basketane, and penguinone.
Below: To celebrate the 2012 London Olympics, chemists Graham Richards and Antony Williams offered a molecule of five rings. They called it olympicene.

Hateful Spider, (You are quite right. It doesn’t matter a bit how one begins a letter, nor, for the matter of that, how one goes on with it, or even how one ends it — and it comes awfully easy, after a bit, to write coldly — easier, if possible, than to write warmly. For instance, I have been writing to the Dean, on College business, and began the letter ‘Obscure Animalcule,’ and he is foolish enough to pretend to be angry about it, and to say it wasn’t a proper style, and that he will propose to the Vice-Chancellor to expel me from the University: and it is all your fault!)
— Lewis Carroll, letter to Agnes Hull, April 30, 1881
Leonard Gordon noted this interesting pattern in the May 1995 issue of Word Ways. The English names of the first eight positive integers (ONE, TWO, THREE, FOUR, FIVE, SIX, SEVEN, EIGHT) contain altogether 32 letters. The smallest rectangular grid into which they can all be packed, word-search fashion, is 5×5. Because some of the cells serve double duty, the 32 letters “fit” into 25 cells; the ratio of these values is 1.28. This ratio remains remarkably consistent as the list of numbers is extended — here are grids for the first 8, 9, 10, 11, and 12 numbers:
E I G H T O N E E R H T E I G H T F E L E V E N S S E V E N O W T F O U R W S E V E N I N F X W O I F S O I E F I V E E R H T X I S O E I G H T W O N I N E O U G O I T N V O G X N E N I N S E V E N F O U R X I S S E V E N R H W U X V E E U H E V L E W T T H R E E T H R E E T H R E E E N R T N E V E L E 8 words 9 words 10 words 11 words 12 words 32 letters 36 letters 39 letters 45 letters 51 letters 25 cells 28 cells 30 cells 35 cells 40 cells (1.28) (1.29) (1.30) (1.29) (1.28)
Alas, the last one isn’t optimal, Gordon notes. The names ONE through TWELVE will fit into a more compact grid:
T W E L V E F N E X S L O F I V E E U S G N V V R T H R E E O W T E N N
… and that raises the ratio to 1.42 letters per cell.
(Leonard Gordon, “Packing the Cardinals,” Word Ways 28:2 [May 1995], 116.)
There was a young fellow of Trinity
Who found
The number of digits
Gave him the fidgets
So he dropped math and took up divinity.
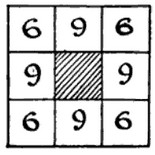
A puzzle by Claude Gaspar Bachet de Méziriac, from 1612, via Henry Dudeney:
A gentleman had a wine-bin of eight compartments, as in the illustration, containing 60 bottles, arranged as shown. His dishonest servant stole 4 bottles and rearranged the remainder. The gentleman noticed that the bottles had been redistributed, but as there were still 21 bottles on every side he innocently concluded that all the 60 were there. The servant, emboldened by his success, again stole 4 bottles and rearranged the remainder without discovery. In fact, on two more occasions he repeated his theft of 4 bottles, always leaving the remainder so arranged symmetrically that there were 21 on every side. How did he arrange them on the four occasions so as to steal the 16 bottles?

In 1971, physicist Joseph C. Hafele and astronomer Richard E. Keating bought airline tickets for a party of four to circle the world twice on commercial airliners. Each party consisted of Hafele, Keating, and two passengers named “Mr. Clock.”
The guests were cesium-beam atomic clocks. The researchers chaperoned the timepieces once eastward around the world and once westward. Then they compared the traveling clocks with one that had remained at the United States Naval Observatory.
The results were published in Science the following year. The clocks had been found to disagree, demonstrating the effects of kinematic and gravitational time dilation.
The total cost of the effort was $8,000. It’s been called one of the most inexpensive tests ever conducted of Einstein’s relativity.
English proverbs:
Experience keeps a dear school. (1743)
Everybody stretches his legs according to the length of his coverlet. (1550)
He that would the daughter win, must with the mother first begin. (1578)
A still tongue makes a wise head. (1562)
Speak not of my debts unless you mean to pay them. (1640)
One of these days is none of these days. (1658)
One hand for yourself and one for the ship. (1799)
It’s never too late to mend. (1590)
The highest branch is not the safest roost. (1563)
He who is absent is always in the wrong. (1640)
The golden age was never the present age. (1732)
Example is better than precept. (1400)
Sweep your own doorstep clean. (1624)
Idle people have the least leisure. (1678)
He that would have eggs must endure the cackling of hens. (1659)
Cockatoos in Sydney have mastered a five-step process for opening the lids of trash bins to reach the food inside.
“It was so exciting to observe such an ingenious and innovative way to access a food resource, we knew immediately that we had to systematically study this unique foraging behavior,” wrote behavioral ecologist Barbara Klump.
The birds learn the technique from one another, and cockatoos in different regions have worked out different techniques. Before 2018, the behavior had been reported in only three suburbs, but by the end of 2019 the number had reached 44.
“These results show the animals really learned the behavior from other cockatoos in their vicinity,” Klump wrote.
(Barbara C. Klump et al. “Innovation and Geographic Spread of a Complex Foraging Culture in an Urban Parrot,” Science 373:6553 [2021], 456-460.) (Thanks, Sharon.)

In June 1809, a ferry boat called the Experiment set out from Providence, R.I. for Pawtuxet Village. It was named for an innovative propulsion system: a screw propeller driven by eight horses on a treadmill. Unfortunately the mechanism was poorly realized — even with a favorable wind and tide, the craft made only 4 knots on her outbound journey, and on the return a gust of wind blew her into mud flats, ending her career. She was broken up and sold to remunerate the creditors, and even the patent was lost in an 1836 fire, but the innovation of the screw propeller would find a place in other designs.
When CNN was launched in 1980, founder Ted Turner said, “Barring satellite problems, we won’t be signing off until the world ends. We’ll be on, and we will cover it live, and that will be our last, last event. We’ll play the National Anthem only one time, on the first of June [1980], and when the end of the world comes, we’ll play ‘Nearer My God to Thee’ before we sign off.”
He wasn’t joking — Turner had ordered the creation of a video of the Christian hymn performed by members of the U.S. Army, Navy, Air Force, and Marine bands. It was held in the network’s archives, marked HFR [Hold For Release] till end of the world confirmed. Michael Ballaban, who’d been an intern at the network’s launch, released the recording above in 2015.
Ballaban wrote, “That leaves open a whole host of unanswered questions. If this is the last CNN employee alive, in the last CNN bureau on Earth, who do they confirm it with? What does confirmation look like? Who can be the one to make that determination, to pronounce the universe itself dead? … And who would be around to watch it? We don’t know.”