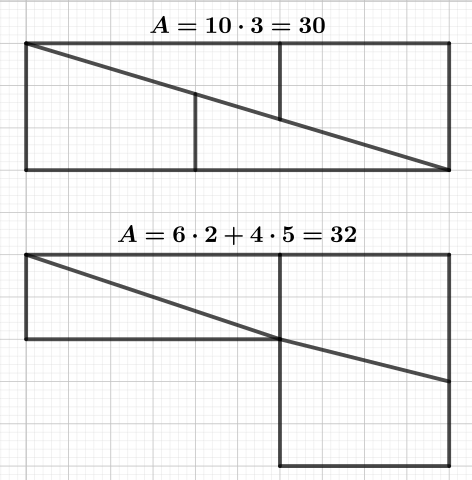
Until 1934, Peñón de Vélez de la Gomera was a Spanish island off the coast of North Africa.
But then a thunderstorm washed enough sand into the channel to create an isthmus to the Moroccan shore.
So now the island is a Spanish exclave on a peninsula, and the two nations share the world’s shortest border.