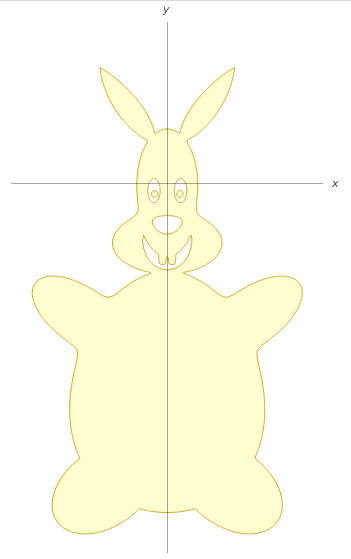
Wolfram Alpha offers some surprising seasonal equations — a bunny:
max(min(-51/25 abs(-(21 x)/(22 a) – (5 y)/(17 a) + 2/11)^(29/16) – 37/17 abs((5 x)/(17 a) – (21 y)/(22 a) + 15/17)^(35/23) + 1, -75/22 abs(-(12 x)/(17 a) – (12 y)/(17 a) + 19/24)^(34/15) – 105/13 abs(-(12 x)/(17 a) + (12 y)/(17 a) + 1/34)^(123/62) + 1, x/a), min(-51/25 abs((21 x)/(22 a) – (5 y)/(17 a) + 2/11)^(29/16) – 37/17 abs(-(5 x)/(17 a) – (21 y)/(22 a) + 15/17)^(35/23) + 1, -75/22 abs((12 x)/(17 a) – (12 y)/(17 a) + 19/24)^(34/15) – 105/13 abs((12 x)/(17 a) + (12 y)/(17 a) + 1/34)^(123/62) + 1, -x/a), min(max(-(177 x^2)/(13 a^2) – 46/15 (y/a + 1/24)^2 + 1, (690 x^2)/(29 a^2) + 63/4 (y/a + 8/17)^2 – 1), 1/10 – ((79 x^2)/(16 a^2) + 16 (y/a + 1/2)^2 – 1) ((16 x^2)/a^2 + (79 y^2)/(16 a^2) – 1), 6287/17 (x/a – 1/9)^2 + 100 (y/a + 1/16)^2 – 1, 6287/17 (x/a + 1/9)^2 + 100 (y/a + 1/16)^2 – 1), -31550/23 (x/a – 2/19)^2 – 62500/49 (y/a + 1/11)^2 + 1, -31550/23 (x/a + 2/19)^2 – 62500/49 (y/a + 1/11)^2 + 1, -18407811/17 (x/a – 1/25)^4 – 250127/15 (y/a + 13/22)^4 + 1, -18407811/17 (x/a + 1/25)^4 – 250127/15 (y/a + 13/22)^4 + 1, -(x/a – 1/2)^2 – (y/a + 5/4)^2 + 1/30, 11/20 – ((y^4/(63 a^4) – y^3/(11 a^3) – y^2/(7 a^2) + (13 y)/(15 a) + x^2/a^2 + 29/43) ((142 x^2)/(15 a^2) + ((-(304 y)/(23 a) – 878/31) x)/a + (1019 y)/(25 a) + (184 y^2)/(13 a^2) + 349/11) ((142 x^2)/(15 a^2) + (((304 y)/(23 a) + 878/31) x)/a + (1019 y)/(25 a) + (184 y^2)/(13 a^2) + 349/11))/(11/19 – y/(8 a))^2, -x^2/a^2 – x/a – (5 y)/(2 a) – y^2/a^2 – 16/9, -(127 x^2)/(21 a^2) – ((-(118 y)/(23 a) – 47/7) x)/a – (559 y)/(15 a) – (173 y^2)/(22 a^2) – 847/19, -(127 x^2)/(21 a^2) – (((118 y)/(23 a) + 47/7) x)/a – (559 y)/(15 a) – (173 y^2)/(22 a^2) – 847/19)>=0
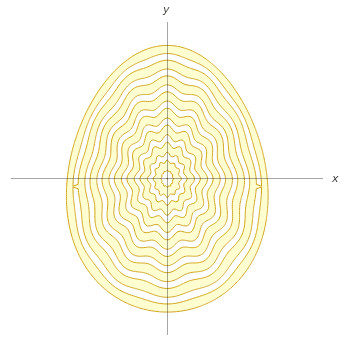
… and an egg:
min(1/5 – sin(16 p sqrt(x^2/(a^2 (1 – y/(10 a))^2) + (9 y^2)/(16 a^2)) (1 – 1/10 (1 – sqrt(x^2/(a^2 (1 – y/(10 a))^2) + (9 y^2)/(16 a^2))) cos(12 tan^(-1)(x/(a (1 – y/(10 a))), (3 y)/(4 a))))), -x^2/(a^2 (1 – y/(10 a))^2) – (9 y^2)/(16 a^2) + 1)>=0
In Poland, Easter Monday is Śmigus-dyngus, in which boys throw water over girls they like and spank them with pussy willow branches. Traditionally, Wikipedia says, “Boys would sneak into girls’ homes at daybreak on Easter Monday and throw containers of water over them while they were still in bed. After all the water had been thrown, the screaming girls would often be dragged to a nearby river or pond for another drenching. Sometimes a girl would be carried out, still in her bed, before both bed and girl were thrown into the water together. Particularly attractive girls could expect to be soaked repeatedly during the day.”
(Thanks, Danesh and Wade.)