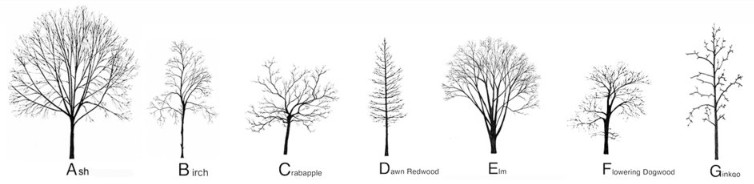
Artist Katie Holten has created a New York City Tree Alphabet, a Latin alphabet in which each letter is assigned a drawing of an existing city tree or one that will be planted as a result of the changing climate. There’s a free font that you can play with here and download here.
Holten had planned to plant messages around the city using real trees last spring, and invited people to make suggestions, though I don’t know which were ultimately chosen. “Right now, we’re leaving it completely wide open, so we’ve no idea what messages we’ll be planting,” she told Fast Company in March. “I’m excited to see what people send us. People have been suggesting words like ‘Dream,’ ‘Hope,’ and ‘Peace.’ But we’re also receiving longer messages, love letters, poems, and short stories. We’re curious to see how we could translate a long text into a grove of planted trees. It’s an exciting challenge and we can make up the rules as we go along, so anything could happen.”
(Via MetaFilter.)