Linguist Ghil’ad Zuckermann writes homophonous poems: One part written in Israeli Hebrew sounds the same as another written in Italian, and both make sense.
(In my notes I see that the same example appeared in Word Ways in November 2003.)
Linguist Ghil’ad Zuckermann writes homophonous poems: One part written in Israeli Hebrew sounds the same as another written in Italian, and both make sense.
(In my notes I see that the same example appeared in Word Ways in November 2003.)
O blessed Letters, that combine in one
All ages past, and make one live with all:
By you we doe conferre with who are gone,
And the dead-living unto councell call:
By you th’ unborne shall have communion
Of what we feele, and what doth us befall.
— Samuel Daniel, Musophilus, 1599

This is just a detail that I found interesting — early regulator clocks tended to slow down as their pendulums lengthened in warm conditions. One solution, offered by George Graham in 1721, was to attach two vials of mercury to the pendulum — as the pendulum warmed and expanded, so did the mercury, creeping upward in its vials and, at least in theory, preserving the pendulum’s center of mass.
One difficulty is that the mercury tends to warm more slowly than the pendulum itself, but the system worked well enough to persist into the 20th century.
From the MapPorn subreddit:
In 1789 political theorist Emmanuel Joseph Sieyès proposed dividing France into an egalitarian checkerboard of departments, cantons, and communes, following a plan conceived in 1780 by royal cartographer Robert de Hesseln.
The assembly rejected the proposal and adopted one that more closely followed the natural boundaries formed by geography and established by historical precedent.

Binghamton University English professor Michael Sharp has been blogging about the New York Times crossword puzzle every day since 2006 under the name Rex Parker. He downloads each puzzle when it becomes available at 10 p.m. and typically solves it in 3-10 minutes.
His blog, Rex Parker Does the NY Times Crossword Puzzle, has become so popular that there’s now a metric website that analyzes his opinions:
“It’s like a little present,” he told the Chronicle of Higher Education last year. “You have no idea what’s in there. And if you’re lucky, something weird or strange or funny is in there. And you get to unwrap this little present every day that will make your brain light up in weird ways if it’s done right.”
(Thanks, Laura.)
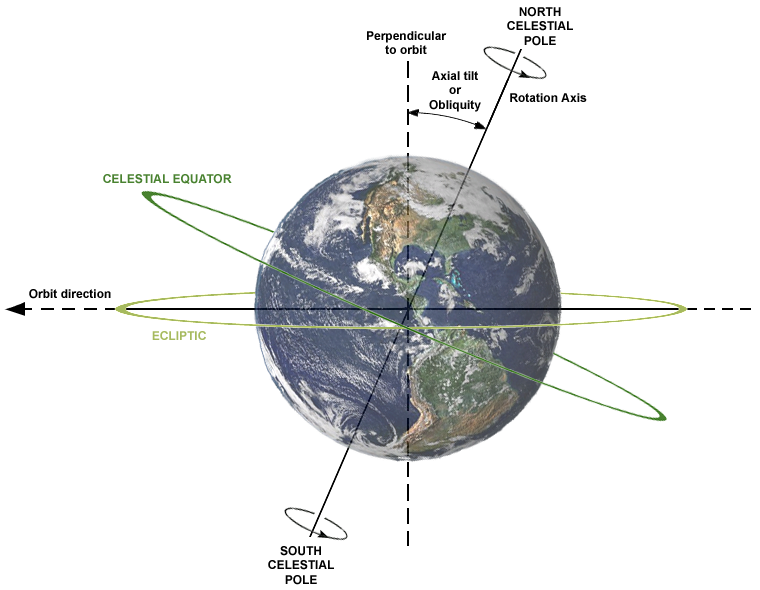
A neat astronomy fact: At the equinox, the sun rises due east and sets due west at every latitude on Earth (except at the poles, where east and west are undefined).
The celestial equator is the great circle writ on the sky above our own equator. For any point on Earth (except the poles), due east and due west mark the intersection of that circle with the horizon. At the equinox the sun is on the celestial equator, so it rises due east and sets due west, not just on our equator but everywhere.
(Thanks, Sanford.)

Below the Japanese village of Aneyoshi, a 4-foot stone has stood since 1933. “Do not build your homes below this point!” it reads. “High dwellings ensure the peace and happiness of our descendants.” The village had already been devastated by a tsunami in 1896, and after a second blow the residents erected a permanent warning to those who would follow them.
It worked. A record-setting tsunami in 2011 destroyed hundreds of miles of the coast but stopped 300 feet below the Aneyoshi stone. “They knew the horrors of tsunamis,” village leader Tamishige Kimura told the New York Times, “so they erected that stone to warn us.”

When Michelangelo’s David was unveiled in 1504, it was seen to symbolize the civil liberties of the Republic of Florence in the face of the surrounding city-states and the powerful Medici.
A Medici duke commissioned Cellini’s Perseus With the Head of Medusa, which was unveiled 50 years later. Composed of bronze, it was situated opposite the David — so that Medusa’s gaze seemed to turn it to stone.

In 1909, 22-year-old Alice Huyler Ramsey set out to become the first woman to drive across the United States. In an era of imperfect cars and atrocious roads, she would have to find her own way and undertake her own repairs across 3,800 miles of rugged, poorly mapped terrain. In this week’s episode of the Futility Closet podcast we’ll follow Ramsey on her historic journey.
We’ll also ponder the limits of free speech and puzzle over some banned candy.
jouisance
n. use or enjoyment
Barmecidal
adj. giving only the illusion of plenty
cacœconomy
n. bad management
furibund
adj. irate
The residents of the parking-challenged Hampshire town of Farnborough were delighted in 2016 to learn that a fully equipped car park had been lying unused for five years. The bad news: It could be reached only on foot. It resides on a roof above a gym complex.
Under the plan, motorists would reach the facility via a bridge from an adjoining property. But that site was still under development.
“We have a massive problem with car parking in Farnborough,” councillor Gareth Lyon told the Independent. “To have had this huge car park lying empty defies belief. It is ridiculous.”
(Thanks, Charlie.)