
“Comparison is the thief of joy.” — Theodore Roosevelt

“Comparison is the thief of joy.” — Theodore Roosevelt

The first woman to circumnavigate the world did so dressed as a man. In 1766, 26-year-old Jeanne Baret joined a French expedition hoping to conceal her identity for three years. In this week’s episode of the Futility Closet podcast we’ll tell the story of her historic journey around the globe.
We’ll also hear Mark Twain’s shark story and puzzle over a foiled con artist.
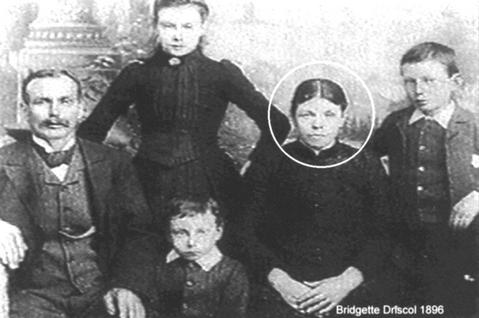
On Aug. 17, 1896, 44-year-old Bridget Driscoll was crossing Dolphin Terrace on the grounds of London’s Crystal Palace when she was struck and killed by a car belonging to the Anglo-French Motor Carriage Company.
The car had been traveling at 4 mph, “a reckless pace, in fact, like a fire engine,” according to one witness.
After a six-hour inquest, the jury returned a verdict of accidental death. Coroner Percy Morrison said he hoped such a thing “would never happen again.”

In 2005 the Austrian art group Gelitin offered the “Tantamounter,” a sealed wooden box the size of a small house. Visitors could place any object into a hatch, and within an hour a handmade “duplicate” would join it. More examples.
In 2004 they built a roller coaster inside a Milan gallery (below).
From a collection in Frank Mittler’s Little Book of Word Tricks (1958):
1. Pray tell me, listener, if you can,
Who is that highly-favored man
Who, though he marries many a wife,
May still stay single all his life?
2. I sit in fire, but not in the flame;
I follow the master, but not the dame;
I’m found in the church, but not in the steeple;
I belong to the monarch, but not the people.
3. Its light was mellow, soft and lazy;
One foot broke off — and it went crazy!
4. What is found in the very center of both America and Australia?
5. What divides by uniting and unites by dividing?
6. Why is a popular crooner like a doctor in an asylum?

When electricity first became widely available, it was hailed as marvel, more valuable even than a human servant. In a 1914 manual on using electricity in the home, Maud Lancaster wrote:
[I]t is always at hand; always willing to do its allotted task and do it perfectly silently, swiftly and without mess; never wants a day off, never answers back, is never laid up, never asks for a rise; in fact it is often willing to work for less money; never gives notice and does not mind working overtime; it has no prejudices and is prepared to undertake any duties for which it is adapted; it costs nothing when it is not actually doing useful work.
First, though, people had to learn to use it. In 1884, electrical engineer Rookes Crompton wrote, “At the recent Crystal Palace Electrical Exhibition, a couple from the country asked the price of an incandescent lamp at one of the stalls, and being supplied with it for 5s., expended a box of matches in trying to light it, and then declared the whole thing was a swindle.”
“Not ignorance, but ignorance of ignorance, is the death of knowledge.” — Alfred North Whitehead
In 1958, momentarily exasperated at the jargon that afflicted behavioral science, Harvard sociologist Daniel Bell typed up an impenetrable paper titled “The Parameters of Social Movements: A Formal Paradigm”:
The purpose of this scheme is to present a taxonomic dichotomization which would allow for unilinear comparisons. In this fashion we could hope to distinguish the relevant variables which determine the functional specificities of social movements. Any classificatory scheme is, essentially, an answer to some implicit other scheme. In this instance, it is an attempt to answer the various hylozoic theories which deny that social categories can be separable.
He divided social movements into two types, the homologous and the metonymous. Homologous movements are distinguished by structural variables (monocotyledonous and dicotyledonous), matrix variables (ultramontane and anti-nomian), and process variables (syncretistic and diastrophic). Metonymous movements, by contrast, are marked by goal definitions (transcendental or eschatological), a matrix of change that’s quietistic or chiliastic (the latter either sectarian or lacrimatarian), and a mode of change that’s immanent or informed by kairos (diastasis).
“I sent it off to two sociological friends, who I thought would appreciate it, and one sent me back a serious letter about some of the categories, while the other, not knowing whether it was a spoof or not, wrote: ‘You are too good a sociologist not to have created something which itself is quite useful.'”
(From Dwight Macdonald, Parodies, 1960.)
Alexandra Kehayoglou makes carpets that evoke the topography of her native Argentina: grasslands, waterways, and glaciers. Her family opened a conventional carpet company there in 1956, and she discovered she could use scraps from their work to create “tactile canvases.” Each piece is composed by hand from discarded or surplus wool on a vertical frame, using a tufting gun and carpet scissors.
Her work often draws attention to natural areas altered by human activity in Argentina, such as the Raggio Creek north of Buenos Aires, destroyed for a shopping mall, or the Santa Cruz River, the last free-flowing wild river in the country, proposed site of two major hydroelectricity dams.
“It’s hard for people to understand that a rug can be art,” she told the New York Times. “But maybe that’s changing.”

Mike Keith published this remarkable invention in the Journal of Recreational Mathematics in 1975. Suppose a chess game goes:
P-K4 P-K4 B-B4 P-R4 Q-B3 P-R4 QxP
This is checkmate, so White says “I win!” Now if the game score is written out in one column, including White’s exclamation:
P-K4 P-K4 B-B4 P-R4 Q-B3 P-R4 QxP ---- IWIN
… we get a solvable alphametic — replace each letter (and the symbols x and -) with a unique digit and you get a valid sum. (The digits already shown count as numbers, and those numbers also remain available to replace letters.)
This example isn’t quite perfect — the two moves P-R4 are ambiguous, as is the final pawn capture. Keith’s Alphametics Page has an even better specimen, a pretty variation from a real 1912 game by Siegbert Tarrasch. It’s 13 moves long and forms a perfect alphametic with a unique solution.