
When William Makepeace Thackeray was five years old, his aunt was alarmed to discover that his uncle’s hat fit him.
“Don’t be afraid,” the doctor told her. “He has a large head, but there’s a good deal in it.”

When William Makepeace Thackeray was five years old, his aunt was alarmed to discover that his uncle’s hat fit him.
“Don’t be afraid,” the doctor told her. “He has a large head, but there’s a good deal in it.”
French acrobat and dancer Yoann Bourgeois created Celui qui tombe for the 2014 International Dance Biennial of Lyon. He calls the six dancers “a mankind in miniature.”
“It’s clear that if you do it ‘your way’ rather than the group’s way, you imperil and unbalance the joint venture,” wrote Luke Jennings in a Guardian review. “But you also get freedom. Or do you?”

A “no-brainer” by Harvard mathematician (and chess master) Noam Elkies. White has choices as to how to play, but no matter how he proceeds, he’ll wind up mating Black on the seventh move.
(From Tim Krabbé’s chess diary.)

Union general Joseph Hooker had an eventful day at the Battle of Chancellorsville:
I was standing on this step of the portico on the Sunday morning of the 3d of May, and was giving direction to the battle, which was now raging with great fury, the cannon-balls reaching me from both the east and the west, when a solid shot struck the pillar near me, splitting it in two, and throwing one-half longitudinally against me, striking my whole right side, which soon turned livid. For a few moments I was senseless, and the report spread that I had been killed. But I soon revived, and to correct the misapprehension, I insisted on being lifted upon my horse, and rode back towards the white house, which subsequently became the center of my new position. Just before reaching it, the pain from my hurt became so intense, that I was likely to fall, when I was assisted to dismount, and was laid upon a blanket spread out upon the ground, and was given some brandy. This revived me, and I was assisted to remount. Scarcely was I off the blanket, when a solid shot, fired by the enemy at Hazel Grove, struck in the very center of that blanket, where I had a moment before been lying, and tore up the earth in a savage way.
In Strange Tales of the Civil War, Michael Sanders writes, “In this way, Joseph Hooker avoided being instantly killed by two cannon balls within minutes of each other.”

Four years ago, the city was making extensive repairs for a number of blocks along our main thoroughfare here in Pasadena, putting in a complete new set of pipes. After two weeks, the day came when I was to have my hair done. I heard machinery in the distance, but decided to go on.
I soon found myself right in the midst of the work which was plenty noisy. Rene was on the outside, the side of the machinery, but aside from slowing up a little, she kept steadily on her way. One of the workmen shouted that the dog was doing fine, but I noticed that she kept pushing me very close to the buildings, almost against them. When I reached the shop and mentioned the way we had come, everyone was simply horrified. All along the block where Rene had kept me so close the buildings was just a narrow strip of sidewalk. The rest was a great hole where pipes were being laid.
— Genevieve Wiley on her dog Rene, from Peter Brock Putnam, Love in the Lead: The Fifty-Year Miracle of the Seeing Eye Dog, 1979

Canada’s René-Levasseur Island is larger than the lake that surrounds it.
The island occupies 2,020 square kilometers, while the surrounding Lake Manicouagan covers 1,942.
Visible from space, the feature is sometimes called the Eye of Quebec.
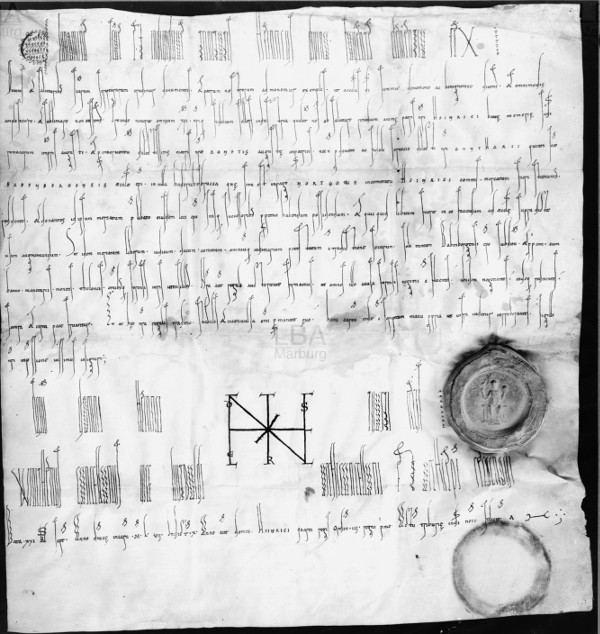
The framers of medieval charters needed to make them visually striking and memorable — relatively few people would be able to understand the Latin legalities, but many would see the documents, and in order to carry authority they had to look different from ordinary texts, remarkable and unique.
One way to do this was with “an altogether peculiar sort of writing, of which the first characteristic is elongation,” writes Nicolete Gray in Lettering as Drawing. In this charter given by Holy Roman Emperor Henry IV to the bishopric of Bamberg in 1057, the text is written in long, attenuated letters:
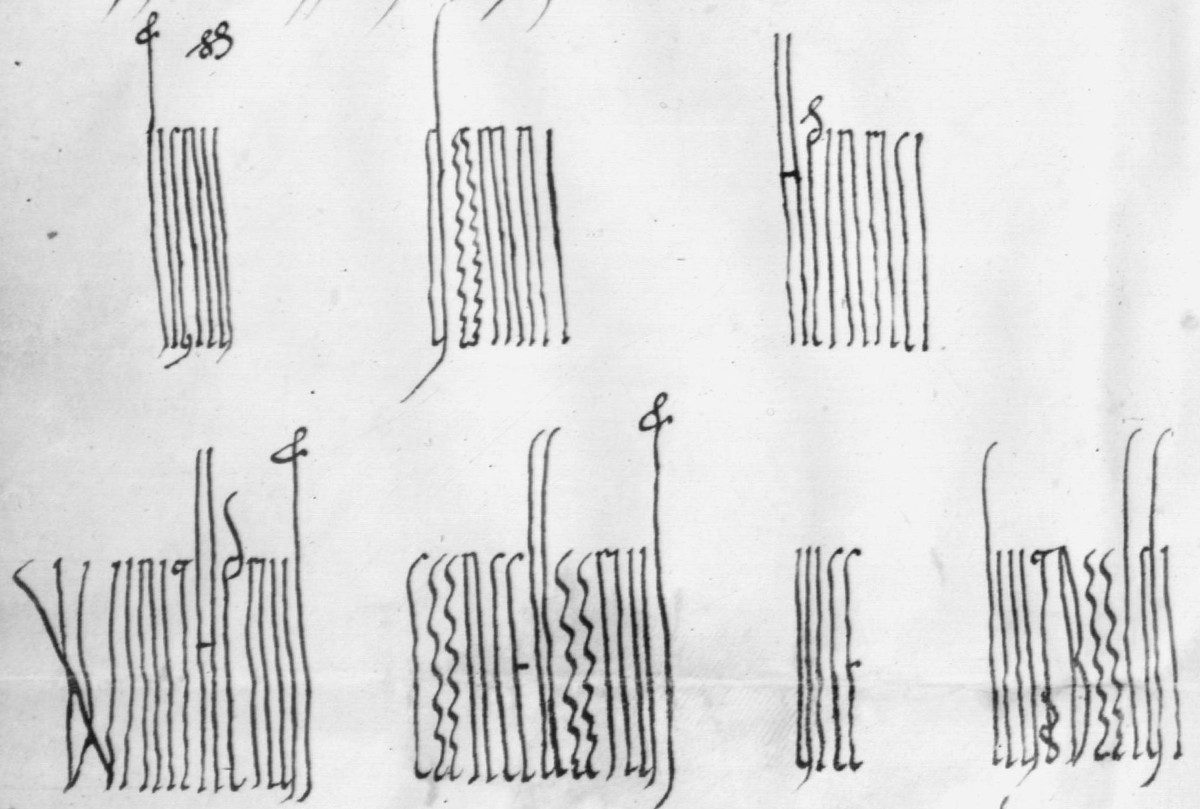
“The strange letter forms impress themselves, due to their difference from the norm, on the peoples’ consciousness and they thus endow the charter with a kind of aura that sets it apart,” writes Laurence de Looze in The Letter & the Cosmos. The signatures were often elaborate for the same reason: “A trace of worldly power is carried over into the writing, the letter forms performing this transfer of the power from the people who created the charter into the document itself.”

I say that conceit is just as natural a thing to human minds as a centre is to a circle. But little-minded people’s thoughts move in such small circles that five minutes’ conversation gives you an arc long enough to determine their whole curve. An arc in the movement of a large intellect does not sensibly differ from a straight line. Even if it have the third vowel [‘I’, the first-person pronoun] as its centre, it does not soon betray it. The highest thought, that is, is the most seemingly impersonal; it does not obviously imply any individual centre.
— Oliver Wendell Holmes Sr., The Autocrat of the Breakfast-Table, 1858

After starring as the title character, Anne Shirley, in the 1934 film Anne of Green Gables, actress Dawn O’Day changed her stage name to Anne Shirley and used it for the rest of her career.
On April 10, 1886, Edward Elgar visited the Crystal Palace to attend a performance in honor of 75-year-old Franz Liszt, who was visiting England after an absence of many years. In the margin of his program Elgar made a cryptic notation:

What does it mean? Anthony Thorley suggested that it was a cipher representing the words GETS YOU TO JOY, AND HYSTERIOUS, where the last word is a portmanteau combining hysteria and mysterious. But that seems contrived, and in any case “this doesn’t fit!” writes Craig Bauer in Unsolved!, his history of ciphers. “Not only do repeated letters fail to line up with the same squiggles each time, but we don’t even have the right number of squiggles. The last six letters of the proposed decipherment have nothing to line up with.”

If Thorley is mistaken, then this fragment remains unsolved, like Elgar’s Dorabella cipher of 11 years later. Are the two messages related?