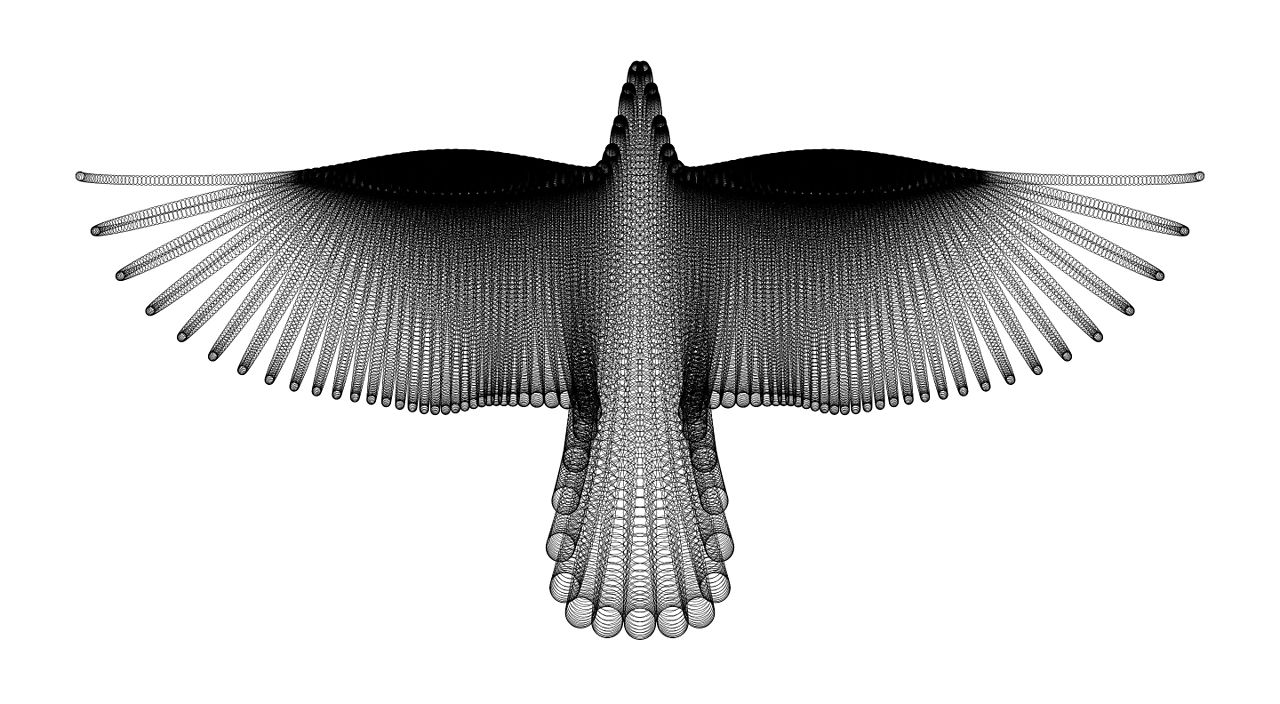
Iranian artist Hamid Naderi Yeganeh makes art from math. The image above shows all circles of the form , for k = -10000, -9999, … , 9999, 10000, where

Iranian artist Hamid Naderi Yeganeh makes art from math. The image above shows all circles of the form , for k = -10000, -9999, … , 9999, 10000, where
In 1927, Ukrainian conductor Nikolai Malko played Vincent Youmans’ song “Tea for Two” for Dmitri Shostakovich and bet 100 roubles that the composer couldn’t reorchestrate it from memory in less than an hour.
Shostakovich did it in 45 minutes.
He later incorporated the arrangement into Tahiti Trot and used it as an entr’acte in his 1930 ballet The Golden Age.
(Thanks, Allen.)
In the 1950s, archaeologists unearthed a cuneiform tablet from an ancient palace in northern Syria. Dating to 1400 BC, it contained lyrics for a hymn to Nikkal, a Semitic goddess of orchards, as well as instructions for a singer accompanied by a nine-stringed lyre.
That makes the “Hurrian hymn” the oldest surviving example of a written song.
When Colonel Abraham Holmes, a supporter of Monmouth, was executed with some of his companions at Lyme Regis in 1685, the horses could not pull the sled carrying the condemned men to the scaffold. The attendants began to whip them furiously, whereupon Colonel Holmes, with one of those superb gestures of which the men of the seventeenth century were so frequently capable, got out to walk, saying, ‘Come, gentlemen, don’t let the poor creatures suffer on our account. I have often led you in the field. Let me lead you on in our way to Heaven.’
— Keith Thomas, Man and the Natural World, 1983

In 1973 Anthony Burgess lost a book manuscript to a scippatore, a thief on a Vespa.
He was living in Rome and working on Joysprick, his study of the language in Finnegans Wake. “I carried it in its Gucci case towards a Xeroxshop to be copied, but it was scippato on the way.”
He was remarkably philosophical about the loss. “The typescript was presumably fluttered into the Tiber or Tevere and the case sold for a few thousand lire. I had to write the book again, not with too much resentment: it was probably better the second time.”
“These scippatori were never caught by the police, who probably shared in their proceeds: their little motorcycles were not legally obliged to be fitted with a targa or numberplate. Petty crime is excused, or even exalted, by the greater crimes of the Quirinale.”
(From Burgess’ memoir You’ve Had Your Time, 1990.)

To show that soil can be transformed into habitable architecture, Colombian artist Octavio Mendoza made a 5,400-square-foot house entirely out of clay. Casa Terracota (known to the neighbors as “Casa de Flintstones”) contains no cement or steel — the whole building is fashioned from clay, including two floors of living space, all the furniture, and all the dishes.
After a career spent designing more conventional buildings, Mendoza spent 14 years realizing the project, to show that functional buildings can be made using the natural resources at hand. He calls it “the biggest piece of pottery in the world.”

Then God said, Let there be light! And the light came. And God saw the light, and it pleased him, and he gave it the name of Day. And when the day was gone, and the dark came back to stay for a while, he gave the dark spell the name of Night. And God did these things on the first day.
— Josephine Pollard, History of the Old Testament in Words of One Syllable, 1888
04/20/2018 UPDATE: Much later, in 1994, MIT logician George Boolos summarized Gödel’s second incompleteness theorem in words of one syllable. (Thanks, Ethan.)

“According to the legend whispered by the retainers and villagers, no sooner did the clock strike twelve than a headless apparition was seen to move slowly across the moonlit hall.”
In 1911 English humorists Edward Verrall Lucas and George Morrow took the illustrations from a department store catalog and arranged them into “a deeply-moving human drama.”
Stewart C. Russell has put the whole thing online (PDF).
French composer Charles Koechlin rarely watched films until he saw The Blue Angel in 1933 and became captivated by “the formidable realm of the cinema.” He set to work and in a few weeks produced a Seven Stars Symphony, with a movement dedicated to each of seven actors of the day: Douglas Fairbanks, Lilian Harvey, Greta Garbo, Clara Bow, Marlene Dietrich, Emil Jannings, and Charlie Chaplin.
Interestingly, Robert Orledge writes in his biography of the composer, “The fifth, sixth and seventh movements, depicting Marlene Dietrich, Emil Jannings and Charlie Chaplin, are based on a cipher system of Koechlin’s own devising, in which the themes spell out the stars’ names, and in the case of the Emil Jannings movement virtually tell a film story in music.” I’ll try to find out more about that.