Author: Greg Ross
Men in Aida
In 1983 poet David Melnick reinterpreted the first book of Homer’s Iliad by brutely understanding the spoken Greek as English, producing a bathhouse farce:
Men in Aida, they appeal, eh? A day, O Achilles.
Allow men in, emery Achaians. All gay ethic, eh?
Paul asked if team mousse suck, as Aida, pro, yaps in.
Here on a Tuesday. “Hello,” Rhea to cake Eunice in.
“Hojo” noisy tap as hideous debt to lay at a bully.
Ex you, day. Tap wrote a “D,” a stay. Tenor is Sunday.
Atreides stain axe and Ron and ideas’ll kill you.
In 2015 he published two more books, in each “hearing” Homer’s words as English. He calls it Men in Aïda.
His Mark

While clearing land on his Smithville, Texas, ranch in the late 1990s, cattle farmer Jimmie Luecke wrote his name in letters a kilometer tall, producing the world’s largest signature.
It lies on several major flight paths into Houston, and NASA uses it to evaluate satellite imagery.
Podcast Episode 188: The Bat Bomb

During World War II, the U.S. Army experimented with a bizarre plan: using live bats to firebomb Japanese cities. In this week’s episode of the Futility Closet podcast we’ll describe the crazy history of the bat bomb, the extraordinary brainchild of a Pennsylvania dentist.
We’ll also consider the malleable nature of mental illness and puzzle over an expensive quiz question.
Four of a Kind
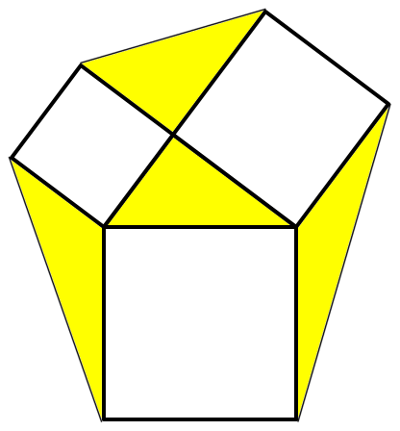
If squares are drawn on the sides of a triangle and external to it, then the areas of the triangles formed between the squares all equal the area of the triangle itself.
(Roger Webster, “Bride’s Chair Revisited,” Mathematical Gazette 78:483 [November 1994], 345-346.)
Special Issue
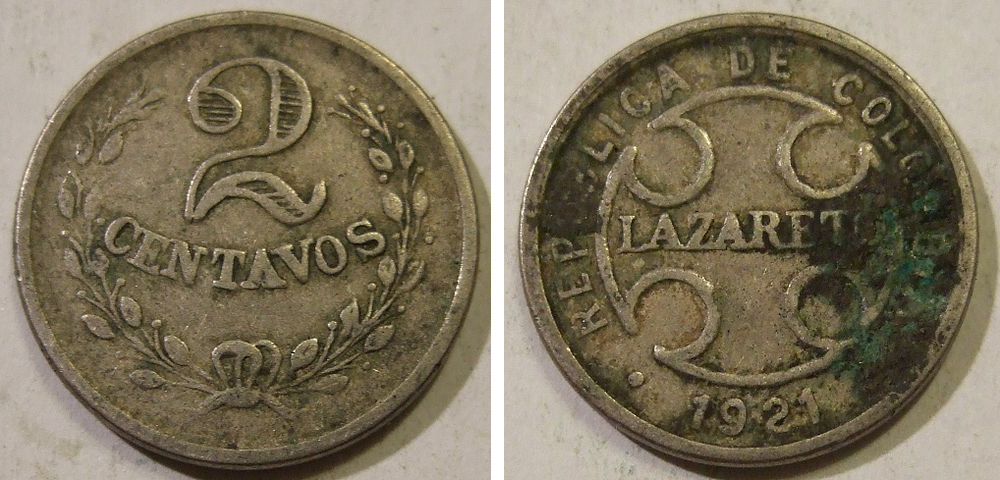
In 1901 Colombia minted special coins for use in leper colonies. Following the first leprosy congress in Berlin in 1897, the nation minted coins in five values for use in three colonies. The Philippines followed suit in 1913, followed by Japan and Malaysia. The United States produced special coins for a colony in the Panama Canal Zone.
The coins were produced to protect healthy people, but in 1938 Gordon Alexander Ryrie, director of Malaysia’s Sungei Buloh Settlement, proved that the disease can’t spread by such casual contact. His colony burned the notes it had printed.
A British Limerick
A young man called Cholmondeley Colquhoun
Kept as a pet a babolquhoun.
His mother said, “Cholmondeley,
Do you think it quite colmondeley
To feed your babolquhoun with a spolquhoun?”
(Via Willard R. Espy.)
Not Dead Yet

The red-crested tree rat hadn’t been seen since 1898 when one turned up at the front door of a Colombian ecolodge in 2011. It posed for photos for two hours and then disappeared again. “He just shuffled up the handrail near where we were sitting and seemed totally unperturbed by all the excitement he was causing,” said volunteer researcher Lizzie Noble. “We are absolutely delighted to have rediscovered such a wonderful creature after just a month of volunteering with ProAves.”
The Bermuda land snail had been thought extinct for 40 years when it turned up in a Hamilton alleyway. “The fact that there was so much concrete around them probably saved them from the predators that we believe killed the vast majority of the population island-wide,” ecologist Mark Outerbridge told the Royal Gazette. “People have been looking for these snails for decades and here they are surrounded by concrete and air conditioners living in a 100-square-foot alleyway in Hamilton.”
The mountain pygmy possum was first identified in a fossil in New South Wales in 1895 and thought to be extinct. Seventy years later, in August 1966, a live pygmy possum was found by chance in a ski hut in the Snowy Mountains of Victoria. R.M. Warneke telegraphed W.D.L. Ride, “BURRAMYS EXTANT STOP NOT REPEAT NOT EXTINCT STOP LIVE MALE CAPTURED MOUNT HOTHAM STOP AM TRYING FOR FEMALE.” The lonely possum died before a companion could be found, but four isolated populations of pygmy possums are now known to persist in the Snowy Mountains.
(Joseph F. Merritt, The Biology of Small Mammals, 2010.)
Math Notes
26072323311568661931
43744839742282591947
118132654413675138222
186378732807587076747
519650114814905002347
Any three of these numbers add up to a perfect square.
(Discovered by Stan Wagon.)
Substitute
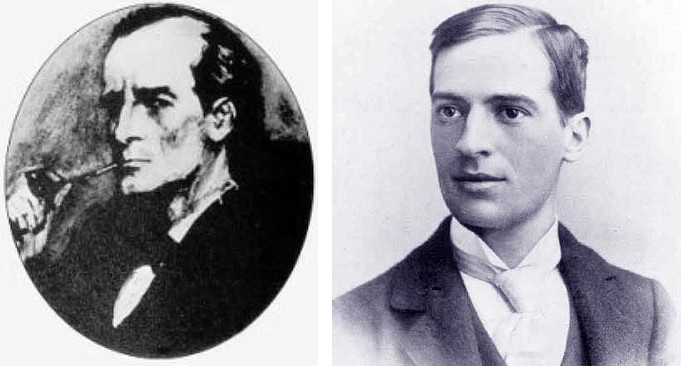
Disguises adopted by Sherlock Holmes:
- “Captain Basil” (“The Adventure of Black Peter”)
- “a common loafer” (“The Beryl Coronet”)
- a rakish young plumber named Escott (“Charles Augustus Milverton”)
- a venerable Italian priest (“The Final Problem”)
- an elderly, deformed bibliophile (“The Empty House”)
- a French ouvrier (“The Disappearance of Lady Frances Carfax”)
- a workman looking for a job, described as “an old sporting man” (“The Mazarin Stone”)
- an old woman (“The Mazarin Stone”)
- a “drunken-looking groom” (“A Scandal in Bohemia”)
- an “amiable and simple-minded” Nonconformist clergyman (“A Scandal in Bohemia”)
- a sailor (The Sign of the Four)
- an asthmatic old master mariner (The Sign of the Four)
- a doddering opium smoker (“The Man With the Twisted Lip”)
- Mr. Harris, an accountant (“The Stock-Broker’s Clerk”)
- a registration agent (“The Crooked Man”)
- a Norwegian explorer named Sigerson (“The Empty House”)
- an Irish-American spy named Altamont (“His Last Bow”)
In 1895 the Brooklyn Chess Club sent young Harry Nelson Pillsbury to England to compete in the great tournament at Hastings. He took first prize but never matched this early success and died in 1906. “Nobody can understand this sudden flash of greatness,” wrote New York Times music critic Harold Schonberg. “A twenty-two-year-old unknown licked the cream of Europe’s experts, trouncing such formidable masters as Lasker, Tarrasch, Tchigorin, Gunsberg and Mieses.” Schonberg suggested that the mystery is easily solved if the victor at Hastings was not Pillsbury but “the finest analytical mind in Europe, the mind of one who had genius, infinite capacity for concentration, and a brilliant insight into chess. Suppose that it was Sherlock Holmes, the master of disguise, who impersonated Pillsbury at Hastings, letting Pillsbury, on his own after that, sink to his normal level.”
(From The Annotated Sherlock Holmes, 1975, and The New Annotated Sherlock Holmes, 2007.)