Sign outside the public library at West Pittston, Pa., October 2016:

Sign outside the public library at West Pittston, Pa., October 2016:

In the 19th century, British polymath William Barnes tried to reform English by limiting it to words of Saxon-English origin. Where no “Teutonic” words were available to express his meaning, he made up alternatives, such as sky-sill for horizon, glee-craft for music, wort-lore for botany, hearsomeness for obedience, somely for plural, and folkwain for omnibus.
In 1948, Richard Lister challenged the readers of the New Statesman to write the opening paragraphs of a novel set in present-day London in this style of reformed English. Reader D.M. Low offered this:
As Ernest was wafted up on the dredger from the thorough-hole at Kingsway he was inwardly upborne to see Pearl again; but, alas, evenly castdown for the blue-eyed bebrilled booklearner was floating downwards on the other ladderway. It was now or never. Ernest fought back against the rising stairs and the gainbuildfulness of hirelings bound for work. Pushing aside fingerwriters, shophelpers and even deeded reckoning-keepers, by an overmanly try he reached the bottom eventimeously with Pearl.
‘What luck! Can you eat with me tonight? I know a fair little upstaker near here.’
‘Oh! I can’t. My Between-go is in Fogmonth, and I must get through and …’
The rumble of the ambercrafty wagonsnake drowned her words.
‘Hark! There’s the tug. I must fly.’
It was hard to be wisdomlustful. Forlorn in his trystlessness Ernest sought Kingsway again and dodging hire-shiners and other self-shifters recklessly headed towards the worldheadtownly manystreakiness of the Strand.
He appended this glossary:
dredger: escalator.
ladderway: escalator.
upborne: elated.
evenly: equally.
bebrilled: bespectacled, (German Brille).
booklearner: student.
gainbuildfulness: obstructiveness.
fingerwriters: typists, cf. dattilografa.
deeded reckoning keepers: chartered accountants.
overmanly: superhuman.
eventimeously: simultaneously.
upstaker (less correctly upstoker): restaurant.
Between go: student slang for Between while try out i.e., Intermediate Examination.
Fogmonth: November.
ambercrafty: electric, lit. electric powered.
wagonsnake: train (archaic and poet.).
tug: train cf. German Zug.
wisdomlustful: philosophical.
trystlessness: disappointment.
hire-shiners: taxis.
self-shifters: automobiles.
manystreakiness: variety.
worldheadtownly: cosmopolitan.
Other readers had suggested eyebiting for attractive, lip-hair for moustache, slidehorn for trombone, and smokeweed for cigarette. The winning entries are here.

Socrates wants to cross a river and comes to a bridge guarded by Plato. The two speak as follows:
Plato: ‘Socrates, if in the first proposition which you utter, you speak the truth, I will permit you to cross. But surely, if you speak falsely, I shall throw you into the water.’
Socrates: ‘You will throw me into the water.’
Jean Buridan posed this conundrum in his Sophismata in the 14th century. Like a similar paradox in Don Quixote, it seems to leave the guardian in an impossible position — whether Socrates speaks truly or falsely, it would seem, the promise cannot be fulfilled.
Some readers offered a wry solution: Wait until he’s crossed the bridge, and then throw him in.
Another blue plaque, this one in Long Itchington, October 2014:

Related: Riverside, Iowa, is already congratulating itself as the future birthplace of James T. Kirk.
Billy Wilder’s grave, Westwood Village Memorial Park Cemetery, Los Angeles:


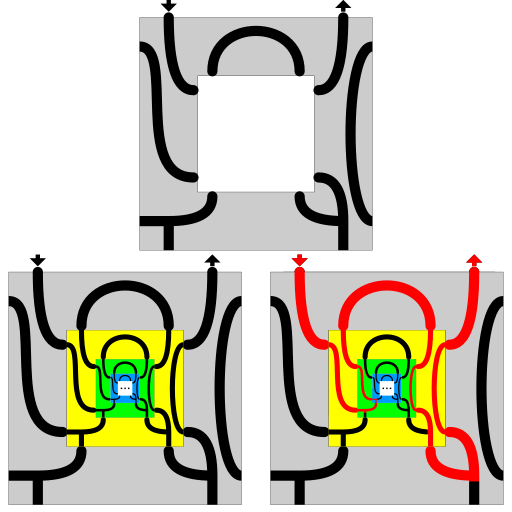
Above: A valid maze can be generated recursively by dividing an open chamber with walls and creating an opening at random within each wall, ensuring that a route can be found through the chamber. The secondary chambers themselves can then be divided with further walls, following the same principle, to any level of complexity.
Below: Valid mazes can even be generated fractally — here a solution becomes available in the third panel, but an unlucky solver might wander forever in the depths of self-similarity at the center of the image.

Found this on the Wikimedia Commons — a self-obligating graffito.
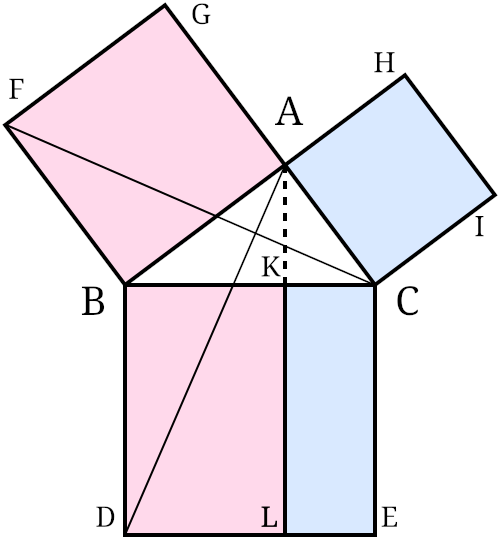
This is Euclid’s proof of the Pythagorean theorem — Schopenhauer called it a “brilliant piece of perversity” for its needless complexity:
The diagram became known as the bride’s chair due to a confusion in translation between Greek and Arabic.

Plaque at St. Ann’s Well, Malvern, Worcestershire, August 2009.
In 1880, an 800-year-old yew tree was threatening the west wall of the church of St Andrew at Buckland in Dover. The community called in landscape gardener William Barron, who solved the problem by boring tunnels under the trunk and then raising the tree’s entire 55-ton mass onto rollers by means of powerful screw jacks. Giant windlasses could then haul the tree 203 feet across the churchard to a safer location.
“The scale of this operation was probably never matched,” writes G.M.F. Drower in Garden of Invention, his 2003 history of gardening innovations. “[A]nd Barron, who had been rather more apprehensive than he let on, later admitted that all the other trees he had moved had been ‘chickens compared to the Buckland Yew.'”