Here’s a lost art: “Ceiling walking” was a popular form of American entertainment as early as 1806, when “Sanches, the Wonderful Antipodean” wore iron shoes that were “fitted in grooves in a board fastened to the top of the stage.”
Spectacles such as this were drawing crowds right through the 19th century. In New Orleans in the 1880s a young “human fly” named Mademoiselle Aimee was carried by her teeth to a trapeze 50 feet in the air, from which she affixed her feet to the ceiling by some indistinct means. “Many such exclamations as ‘My God!’ ‘Oh My!’ and so on follow, and as she puts one foot before the other, walking in a forward direction, the situation is most thrilling,” marveled the Daily Picayune. “Often ladies have fainted at the sight of the almost child’s peril, and men have trembled while looking up at her. Many refuse to look up at all and those who do continue to look are in constant apprehension of a terrible accident. There is no question in the world but that the feat is without parallel in the matter of tempting fate.”
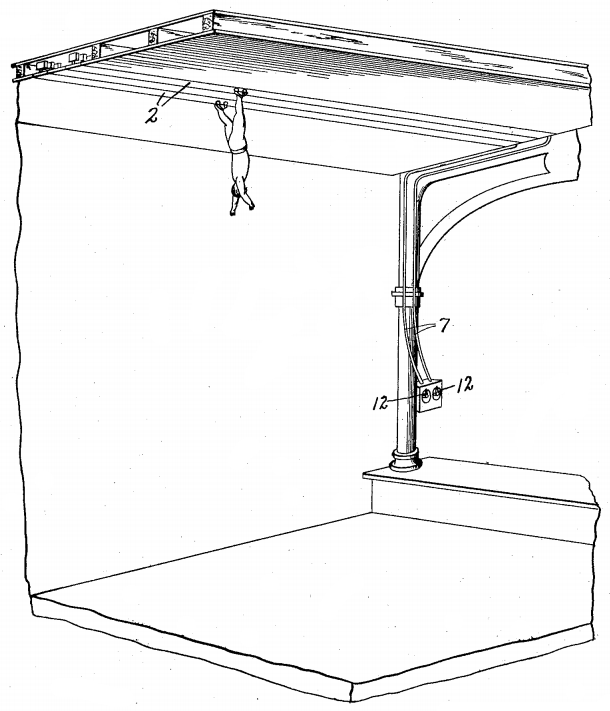
How was this done? There seem to be a range of answers. V. Waid’s “Theatrical Device” of 1905 used vacuum cups attached to the fly’s feet, but both E.I. George’s “Electric Aerial Ambulating System” of 1909 (above) and C.H. Newman and W. Berrigan’s “Electrical Device to Enable Showmen to Walk on the Ceiling” of 1885 used electromagnets.
How would this have evolved if it had remained popular? What would we be using today?
(From Jacob Smith, The Thrill Makers, 2012.)






