Here are two identical rope ladders with slanting rungs. One falls to the floor, the other onto a table. The ladders are released at the same time and fall freely, but the one on the left falls faster, as if the table is “sucking” it downward. Why does this happen?
Author: Greg Ross
Dream Cuisine

In 1973 and 1974, the U.S. armed forces gave a food preference survey to about 4,000 members of the Army, Air Force, Navy, and Marine Corps.
The examiners included three fake dishes “to provide an estimate of how much someone will respond to a word which sounds like a food name or will answer without reading.”
The three fake dishes were “funistrada,” “buttered ermal,” and “braised trake.” The Washington Post reported, “Out of the 378 foods listed, braised trake came in 362, buttered ermal was 356 and funistrada finished several foods above the bottom 40, coming in between brussels sprouts and fried okra.”
For the record, here are the nine lowest-ranked foods, from the bottom up — all nine are so bad that service members ranked them beneath foods that don’t exist at all:
Buttermilk, skimmed milk, fried parsnips, low-calorie soda, mashed rutabagas, french fried carrots, prune juice, stewed prunes, french fried cauliflower.
(“The Ranking of the Favorites,” Washington Post, July 1, 1987. The Army survey is here: PDF.)
Podcast Episode 100: Lateral Thinking Puzzles

Here are five new lateral thinking puzzles to test your wits and stump your friends — play along with us as we try to untangle some perplexing situations using yes-or-no questions.
Watkin’s Folly

In 1890, inspired by France’s new Eiffel Tower, railway entrepreneur Sir Edward Watkin proposed building an even larger tower at Wembley as the centerpiece of a new amusement park there. He sponsored an architectural design competition that attracted 68 designs inspired by everything from the Tower of Pisa to the Great Pyramid of Giza. The winning design, number 37 (center), was to measure 366 meters tall, 45.8 meters taller than Eiffel’s tower. Foundations were laid in 1892, but funding troubles forced a redesign and in the end only the first stage was finished (below). The site was closed in 1902 and the aborted tower was dynamited five years later, but the surrounding park remained popular — it’s now the site of Wembley Stadium.

(Thanks, Meaghan.)
Mallows Bay

About 30 miles south of Washington D.C., on the Maryland side of the Potomac River, lies a curious collection of lozenge-shaped islands, the remains of a mighty fleet of wooden steamships built hurriedly during World War I and made obsolete by the end of the war. The unused ships became the center of a political scandal, “the grandest white elephant” ever built, and for decades the government and various salvage companies dithered over what to do with them. Eventually nature herself decided the question: The sunken hulls had consolidated and enriched the sediment in which they lay, creating a valuable new ecosystem. So the armada remains where it is, the largest collection of wrecked ships in the Western Hemisphere.
(Thanks, Craig.)
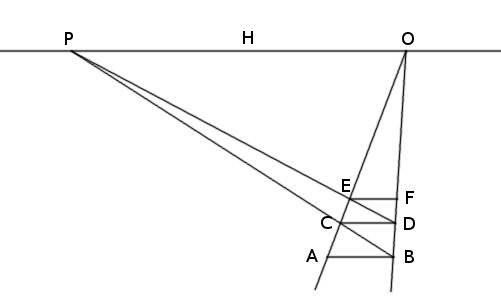
Perspective
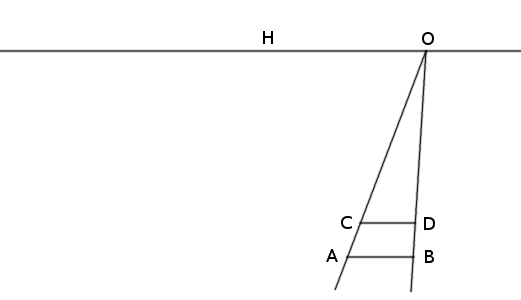
AB and CD are consecutive ties across a pair of railroad tracks that appear to meet at O on the horizon, H. If the ties are parallel to the horizon and are equally spaced along the tracks, how can we draw the next tie in this perspective figure?
As Directed

After being struck by a car in January 1932, Winston Churchill found himself laid up in New York at the height of Prohibition. He convinced his attending physician to write the prescription above.
“I neither want it [brandy] nor need it,” he once said, “but I should think it pretty hazardous to interfere with the ineradicable habit of a lifetime.”
Presto
As military and computer technology exploded in the early 1960s, Raytheon compiled a helpful list of 400 “space-age” abbreviations:
CHAMPION — Compatible Hardware And Milestone Program for Integrating Organizational Needs
COED — Computer Operated Electronic Display
DASTARD — Destroyer Anti-Submarine Transportable ARray Detector
PIPER — Pulsed Intense Plasma for Exploratory Research
It published the list in a booklet titled ABbreviations and Related ACronyms Associated with Defense, Astronautics, Business, and RAdio-electronics — or ABRACADABRA for short.
Literate Art

Spanish artist Jaume Plensa created El Alma del Ebro, above, for a 2008 exposition in Zaragoza on water and sustainable development. (The Ebro River passes through the city.) Visitors can pass in and out of the 11-meter seated figure, but no one has discovered a meaning in the letters that compose it.

Argentine artist Pablo Lehmann cuts words out of (and into) paper and fabric — he spent two years fashioning an entire apartment out of his favorite philosophy books. Reading and Interpretation VIII, above, is a photographic print of Jorge Luis Borges’ “The Garden of Forking Paths” into which Lehmann has cut his own text — a meditation on “the concept of ‘text.'”

In 2011, Buenos Aires native Marta Minujin built a seven-story “Tower of Babel” on a public street to celebrate the city’s designation as a “world book capital.” The tower, 82 feet tall, was made of 30,000 books donated by readers, libraries, and 50 embassies. They were given away to the public after the exhibition.
The Hollowood Function
California high school student Derek Hollowood created this function after considering recurrence relations:
h(-10) = 0.987654321 h(-9) = 0.87654321 h(-8) = 0.7654321 h(-7) = 0.654321 h(-6) = 0.54321 h(-5) = 0.4321 h(-4) = 0.321 h(-3) = 0.21 h(-2) = 0.1 h(-1) = 0 h(0) = 0 h(1) = 1 h(2) = 12 h(3) = 123 h(4) = 1234 h(5) = 12345 h(6) = 123456 h(7) = 1234567 h(8) = 12345678 h(9) = 123456789
(Thanks to Chris Smith for the tip.)