Author: Greg Ross
Emotion and Belief

If you had to judge by bodily sensations alone, could you distinguish shame from embarrassment? Philosopher William Alston suggests that we need to consult our beliefs in order to do this. “Even if there are in fact subtle differences in the patterns of bodily sensation associated with the two, it seems that what in fact forms the basis of the distinction is that it is necessary for shame but not for embarrassment that the subject take the object to be something which is his fault.”
Similarly, Jerome Shaffer proposes that beliefs are necessary to distinguish admiration from envy. Both involve “the belief that the person who is the object of the emotion has some good, but admiration will involve the belief that the person is worthy of it whereas envy will involve the belief that I am worthy of it instead (or, at least, also).”
Robert Yanal suggests that we might even need to check our beliefs in order to distinguish extreme happiness from extreme sadness. “Since both involve a nearly overwhelming rush of sensation, we might know that we are very happy only when we check our belief that our beloved’s life has been spared, not forfeited.” Sensations themselves are not enough to identify the emotion. “Typically, belief or a belief surrogate is brought in to draw the distinctions that we think must be drawn.”
Alston adds that “the presence of such evaluations seems to be what makes bodily states and sensations emotional” in the first place. “Some sinkings in the stomach are emotional, because they stem from an evaluation of something as dangerous; other sinkings are not emotional because they stem from indigestion.”
[William Alston, “Emotion and Feeling,” The Encyclopedia of Philosophy, 1967; Jerome A. Shaffer, “An Assessment of Emotion,” American Philosophical Quarterly, April 1983; Robert Yanal, Paradoxes of Emotion and Fiction, 1999.]
Art and Truth

Is the proposition ‘Botticelli’s Birth of Venus depicts the birth of Venus’ true, false, or neither true nor false? If we assume that there never was such an event as the actual birth of Venus (as we safely can), then this proposition would appear to be analogous to ‘Alexander slew the Minotaur.’ But this proposition is true: Botticelli’s Birth of Venus does depict the birth of Venus.
— W.E. Kennick of Amherst College, posed in Margaret P. Battin et al., Puzzles About Art, 1989
Cancel That
Howard C. Saar of Albion, Mich., pointed out an innovative solution to this problem in Recreational Mathematics Magazine, April 1962:
log(3x + 2) + log(4x – 1) = 2log11
Divide each side of the equation by the word “log”:
(3x + 2) + (4x – 1) = (2)(11)
7x = 21
x = 3
… which is correct.
Presidential Misgivings

George Washington: “So much is expected, so many untoward circumstances may intervene, that I feel an insuperable diffidence in my own abilities.”
John Adams: “If I were to go over my life again, I would be a shoemaker rather than an American statesman.”
Thomas Jefferson called the presidency “a splendid misery.” He said, “To myself, personally, it brings nothing but unceasing drudgery and daily loss of friends.”
John Quincy Adams called his term “the four most miserable years of my life.”
Andrew Jackson: “I can with truth say mine is a situation of dignified slavery.”
Martin Van Buren: “As to the presidency, the two happiest days of my life were those of my entrance upon the office and my surrender of it.”
Buchanan to Lincoln: “”If you are as happy in entering the White House as I shall feel on returning [home], you are a happy man indeed.”
Lincoln: “You have heard about the man tarred and feathered and ridden out of town on a rail? A man in the crowd asked how he liked it, and his reply was that if it wasn’t for the honor of the thing, he would rather have walked.”
Ulysses Grant: “I have been the subject of abuse and slander scarcely ever equaled in political history.”
Rutherford B. Hayes, on leaving office: “The escape from bondage into freedom is grateful indeed to my feelings. … The burden, even with my constitutional cheerfulness, has not been a light one. Now I am glad to be a freed man.”
James Garfield: “My God! What is there in this place that a man should ever want to get into it?”
Grover Cleveland: “I believe I shall buy or rent a house near here, where I can go and be away from this cursed constant grind.”
Teddy Roosevelt, to the incoming Taft: “Ha ha! You are making up your Cabinet. I in a lighthearted way have spent the morning testing the rifles for my African trip. Life has its compensations.”
Taft: “I’ll be damned if I am not getting tired of this. It seems to be the profession of a president simply to hear other people talk.”
Taft to Wilson: “I’m glad to be going — this is the lonesomest place in the world.”
Woodrow Wilson: “I never dreamed such loneliness and desolation of heart possible.”
Warren G. Harding: “This White House is a prison. I can’t get away from the men who dog my footsteps. I am in jail.”
Herbert Hoover: “A few hair shirts are part of the wardrobe of every man. The President differs from other men in that he has a much more extensive wardrobe.”
Harry Truman: “Why in hell does anybody want to be a head of state? Damned if I know.”
Bill Clinton: “Being a president is a lot like running a cemetery: There are a lot of people under you, but nobody’s listening.”
Observations
Excerpts from the notebooks of English belletrist Geoffrey Madan (1895-1947):
Sun sets on 5 May exactly behind the Arc de Triomphe.
There is a social level at which intellect is superfluous; and an intellectual level at which rank is invisible.
The odd fact that one sees Paddington as two such different places when arriving and when departing. [Elsewhere he says this is “perhaps the difference between life seen in youth and old age.”]
“Why is no food blue?” — Jane Asquith (aged 7)
“Society of Contradictory Overseers.” — Attempt by the Chinese Ambassador in 1881 to convey the sense of “Protestant Episcopal Church”
Influenza symptoms seem only a slight intensification of one’s ordinary attitudes to life: disinclination to get up, etc.
“Omlet, Omlet, dies is dein Feyder’s spooke.” — Dutch Hamlet
“My dear, you’re the only woman in the world who’d have known the right hat to wear on an occasion like this.” — Oscar Wilde, to Mrs. Leverson, on his coming out of prison
“De Sancta Cruce”

The English scholar Alcuin devised this remarkable acrostic poem in the ninth century. The text can be read in conventional lines of Latin, and additional phrases are embedded in a symmetrical arrangement of lines that represent the cross inscribed upon the world:
Horizontal, top and bottom:
Crux decus es mundi Iessu de sanguine sancta (“Cross, you are the glory of the world, in Jesus’ blood sanctified”)
Suscipe sic talem rubicumdam celsa coronam (“Accept, exalted cross, from me this scarlet crown”)
Vertical, left and right:
Crux pia vera salus partes in quatuor orbis (“Pious cross, true salvation in the four corners of the world”)
Alma teneto tuam Christo dominane coronam (“Beneficent, take your crown, Christ being the Lord”)
The cross:
Rector in orbe tuis sanavit saecla sigillis (“The ruler of the world saved generations by your sign”)
Surge lavanda tuae sunt saecula fonte fidei (“Rise, the world is cleansed in the font of faith”)
The diamond, representing the world (whose four corners are referenced in the vertical line on the left):
Salve sancta rubens, fregisti vincula mundi (“Hail holy scarlet, you have shattered the world’s shackles”)
Signa valete novis reserata salutibus orbi (“Wonders are manifest, revealed anew to the world in saving works”)
A translation of the full text:
Cross, you are the glory of the world, in Jesus’ blood sanctified.
God the king from the cross conveyed heaven’s judgment.
A victor he reigns, destroying evil and conquering the enemy,
Christ the great sacrifice nailed on the cross for us.
The shepherd by dying redeemed his sheep with his healing right hand.
Glorious, holy salvation from the venerable tree,
he seized the prize, shrugging off the ties of flesh.
Though in bonds the highest king freed us, and he himself
giving his life to the cross triumphed over death,
The kingdom of heaven gaped when the world’s enemy was destroyed.
The sign will be more manifest and all good people will wear it,
praising it with all strength; let all discern more profoundly
so that they may see how many his holy passion frees
from eternal sorrow, and see one thrown down by time
to heal those oppressed by the enemy’s torments; there
may the highest and true Joseph now be our salvation,
who suffered high upon the cross such that error can’t seduce
and poison men and drag them from the light of faith.
The ruler of the world saved generations by your sign.
You, my life, my salvation! For you alone my voice composes hymns,
and shall always sing the highest songs, clear and plain
with the plectrum; for David famous for his song
proves that it is proper for us to testify holiness continually
in elaborate style — accept that which I have just begun, O Christ supernal,
true salvation, great sufferer, you sacred and holy light. Now
the secular nations sing the beneficent sign of the cross,
all the earth trembles and in one accord proclaims
the fame of the cross. In prayer it reveals its inmost heart.
Now hear, vain men, confounded in evil:
The almighty shines forth. May blessed faith fill your hearts
and the serpent not drive them back to their old ways.
The highest and most faithful redeemer has restored us
to his kingdom, and has conquered by this sign the obdurate one,
toppling warlike Satan from the place he hazarded to rule.
Glorious cross, the world should loose its prayers to you.
Accept, exalted cross, from me this scarlet crown.
(From Monumenta Germaniae Historica, part one, 1880, and Jay Hopler and Kimberly Johnson, eds., Before the Door of God: An Anthology of Devotional Poetry, 2013. Thanks, Brandon.)
Podcast Episode 29: The Mystery of Kaspar Hauser

In 1828, a 16-year-old boy appeared in Nuremberg, claiming that he’d spent his whole life alone in a dark cell. In this week’s episode of the Futility Closet podcast we’ll follow the short, sad life of Kaspar Hauser and ponder who he might have been.
We’ll also revisit the Pacific Northwest Tree Octopus, encounter some self-landing planes, and puzzle over why a man would bury 15 luxury cars in the desert.
09/21/2024 UPDATE: New DNA analysis appears to rule out the possibility that Hauser had ties to royal family of Baden. Thanks to listeners Tucker Drake and Charles Hargrove for writing in about this.
In a Word

tonitruation
n. thundering
Finnegans Wake is punctuated by ten thunderclaps, which occur at moments of crisis in the text. “A situation is presented, developed, and subjected to increasing stress until, with the thunder, a collapse, and suddenly a complementary situation that was latent in the first is seen to be in place,” writes scholar Eric McLuhan.
First thunderclap:
bababadalgharaghtakamminaronnonnbronntonnerronnuonnthunn-
trobarrhounawnskawntoohoohoordenenthurknuk
Second:
Perkodhuskurunbarggruauyagokgorlayorgromgremmitghundhurthru-
mathunaradidillifaititillibumullunukkunun
Third:
klikkaklakkaklaskaklopatzklatschabattacreppycrottygraddaghsemmih-
sammihnouithappluddyappladdypkonpkot
Fourth:
Bladyughfoulmoecklenburgwhurawhorascortastrumpapornanennykock-
sapastippatappatupperstrippuckputtanach
Fifth:
Thingcrooklyexineverypasturesixdixlikencehimaroundhersthemagger-
bykinkinkankanwithdownmindlookingated
Sixth:
Lukkedoerendunandurraskewdylooshoofermoyportertooryzooysphalna-
bortansporthaokansakroidverjkapakkapuk
Seventh:
Bothallchoractorschumminaroundgansumuminarumdrumstrumtrumina-
humptadumpwaultopoofoolooderamaunsturnup
Eighth:
Pappappapparrassannuaragheallachnatullaghmonganmacmacmacwhack-
falltherdebblenonthedubblandaddydoodled
Ninth:
husstenhasstencaffincoffintussemtossemdamandamnacosaghcusaghhobix-
hatouxpeswchbechoscashlcarcarcaract
Tenth:
Ullhodturdenweirmudgaardgringnirurdrmolnirfenrirlukkilokkibaugiman-
dodrrerinsurtkrinmgernrackinarockar
Like everything in Joyce, the claps’ meaning is open to question, but they’re not arbitrary: Each of the first nine words contains exactly 100 letters, and the tenth has 101. Joyce, who called thunder “perfect language,” had apparently adjusted the spelling of the thunderclaps as the book took shape: McLuhan found tick marks in Joyce’s galley proofs, “the only evidence of actual letter-counting I have found in any of the manuscripts, typescripts, proofs, and galleys.”
(Eric McLuhan, The Role of Thunder in Finnegans Wake, 1997.)
Catch as Catch Can
Claude Shannon, the father of information theory, took an active interest in juggling. He used to juggle balls while riding a unicycle through the halls of Bell Laboratories, and he built the first juggling robot from an Erector set in the 1970s. (The machine above mimics W.C. Fields, who himself juggled in vaudeville before turning to comedy.)
Noting that juggling seems to appeal to mathematics-minded people, Shannon offered the following theorem:
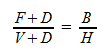
F is flight time, the time the ball spends in the air
D is “dwell time,” the time it spends in the hand
V is vacancy, the time a hand spends empty
B is the number of balls
H is the number of hands
“Theorem 1 allows one to calculate the range of possible periods (time between hand throws) for a given type of uniform juggle and a given time of flight,” he wrote. “A juggler can change this period, while keeping the height of his throws fixed, by increasing dwell time (to increase the period) or reducing dwell time to reduce the period. The total mathematical range available for a given flight time can be obtained by setting D = 0 for minimum range and V = 0 for maximum range in Theorem 1. The ratio of these two extremes is independent of the flight time and dependent only on the number of balls and hands.”
To measure dwell times, Shannon actually created a “jugglometer” in which a juggler wore copper mesh over his fingers and juggled foil-covered lacrosse balls; catching the ball closed a connection between the fingers and started a clock. “Preliminary results from testing a few jugglers indicate that, with ball juggling, vacant time is normally less than dwell time, V ranging in our measurements from fifty to seventy per cent of D.”
Shannon noted that juggling gets dramatically harder as the number of balls increases. He worked out a foolproof solution, at least in theory. A light ray that starts at one focus of an ellipse will be reflected to the other focus. If the ellipse is rotated around its major axis, it will create an egglike shell with two foci. Now if a juggler stands with a hand at each focus, then a ball thrown from either hand, in any direction, will bounce off the shell and arrive at the other hand!
(“Scientific Aspects of Juggling,” in Claude Elwood Shannon: Collected Papers, 1993.)