Does the sequence of squares contain an infinite arithmetic subsequence?
Puzzles
Falling Currency
A problem from the October 1964 issue of Eureka, the journal of the Cambridge University Mathematical Society:
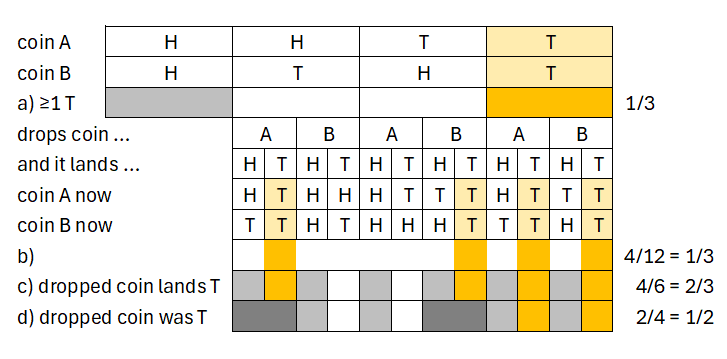
My friend tosses two coins and covers them with his hand. ‘Is there at least one “tail”?’ I ask. He affirms this (a).
Just then he accidentally knocks one of them to the floor (b). On finding the dropped coin under the table, we discover it to be a ‘tail’ (c).
‘That is all right,’ he says, ‘because it was a “tail” to start with.’ (d).
At each point (a), (b), (c) and (d) of this episode I calculated what, to the best of my knowledge, was the probability that both coins showed ‘tails’ at the time. What were these probabilities?
Black and White
Mixed Doubles
In a letter to Maud Standen dated Dec. 18, 1877, Lewis Carroll included a puzzle:
[M]y ‘Anagrammatic Sonnet’ will be new to you. Each line has 4 feet, and each foot is an anagram, i. e., the letters of it can be re-arranged so as to make one word. Thus there are 24 anagrams, which will occupy your leisure moments for some time, I hope. Remember, I don’t limit myself to substantives, as some do. I should consider ‘we dishwished’ a fair anagram.
As to the war, try elm. I tried.
The wig cast in, I went to ride.
‘Ring? Yes.’ We rang. ‘Let’s rap.’ We don’t.
‘O shew her wit!’ As yet she won’t.
Saw eel in Rome. Dry one: he’s wet.
I am dry. O forge! Th’rogue! Why a net?
For example, the first foot in the first line, “As to,” can be rearranged to spell OATS. Carroll left no solution, but he did add a parting riddle to which we have the answer:
“To these you may add ‘abcdefgi,’ which makes a compound word — as good a word as ‘summer-house.'” What is it?
Nonary
Take a whole number, reverse the order of its digits, and subtract one from the other. The difference will always be evenly divisible by 9.
Does this remain true if we just scramble the digits of the first number, rather than reversing them?
A Harrowing Puzzle
A gigantic tire, with a radius of 100 miles, is rolling down Broadway at 60 mph. One driver fails to notice the tire’s approach until its descending surface is just touching the roof of her car, 6 feet above the road. If she leaves the car immediately and can shrink to within 2 feet of the road’s surface, how long does she have to crawl out of the tire’s path?
One Last Christmas Challenge
The Xmas Puzzles 2025 is now live — 13 fiendish puzzles and a “metapuzzle” that draws on their solutions. The competition will run until 20:00 GMT on January 18.
Quizmaster Tim Paulden has pledged just over £1000 in charitable donations as prizes. The top four entries will win a donation to a charity or good cause nominated by the solver: £200 for first place, £150 for second, £120 for third, and £90 for fourth. Those who solve the metapuzzle or score 50 percent or more will also win a donation.
Entry is free and open to all — participants can work alone or in teams of up to five people. Details are at the link above.
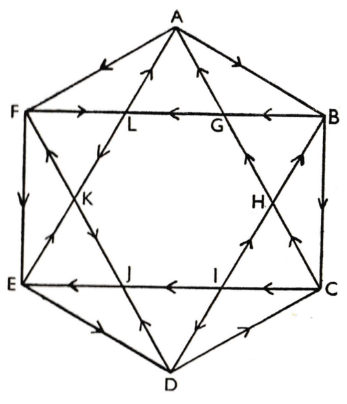
Round Trip
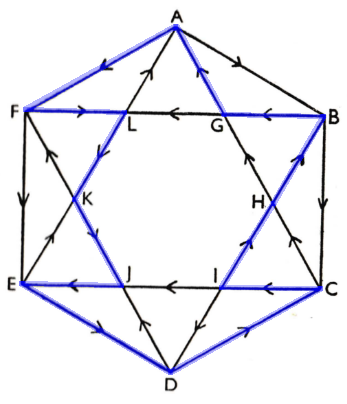
A problem from the October 1961 issue of Eureka, the journal of the Cambridge University Mathematical Society:
“The map below represents one-way street system of a certain university city, the direction in which travel is allowed being indicated by arrows. An undergraduate living at A wishes to cycle round the city, visiting each intersection just once, and returning to A. What route must he take?”
A Chess Maze

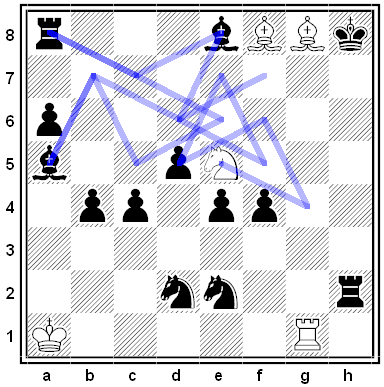
By Daniel Currie Hall. Suppose time stops and the white knight can make as many consecutive moves as it pleases. How quickly can it mate the black king provided that it never moves onto a square on which it’s under attack? (It can make captures, provided it makes them “safely.”)
Another Christmas Quiz
King William’s College, on the Isle of Man, has posted this year’s edition of “The World’s Most Difficult Quiz,” with its customary epigraph, Scire ubi aliquid invenire possis ea demum maxima pars eruditionis est (“The greatest part of knowledge is knowing where to find something”). Some sample questions:
- During 1925, in what was the worrying amnesia of Charles Edward Biffen revealed?
- Where did Ross’s trainer trial tendon-nicking on three sheep?
- Beating, tacking, reaching, luffing or even protesting — what took its name from the long-finned tuna?
- Which Roman edifice was believed to stand above the head of a mythical three-bodied ogre?
- Who was Mr Winterbottom?
- In which Cathedral is illumination seemingly provided by tungsten?
- What name mimicked that of an elite Pullman service, but with a change of weapon?
- Who warned of an explosion in three seconds on his banana night?
- Where was the final resting place of the Bronze Age toxophilite?
Answers will be posted at the end of January.
Usually MetaFilter organizes a Google spreadsheet of communal guesses; if that materializes I’ll post a link here.
12/24/2025 UPDATE: Here’s the MetaFilter thread, and here’s the shared Google doc.