The Renaissance mathematician Niccolò Tartaglia would use this bewildering riddle to assess neophytes in logic:
If half of 5 were 3, what would a third of 10 be?
What’s the answer?
The Renaissance mathematician Niccolò Tartaglia would use this bewildering riddle to assess neophytes in logic:
If half of 5 were 3, what would a third of 10 be?
What’s the answer?

A mother takes two strides to her daughter’s three. If they set out walking together, each starting with the right foot, when will they first step together with the left?
A puzzle by Henry Dudeney:
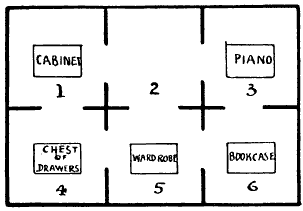
The Dobsons secured apartments at Slocomb-on-Sea. There were six rooms on the same floor, all communicating, as shown in the diagram. The rooms they took were numbers 4, 5, and 6, all facing the sea.
But a little difficulty arose. Mr. Dobson insisted that the piano and the bookcase should change rooms. This was wily, for the Dobsons were not musical, but they wanted to prevent any one else playing the instrument.
Now, the rooms were very small and the pieces of furniture indicated were very big, so that no two of these articles could be got into any room at the same time. How was the exchange to be made with the least possible labour? Suppose, for example, you first move the wardrobe into No. 2; then you can move the bookcase to No. 5 and the piano to No. 6, and so on.
It is a fascinating puzzle, but the landlady had reasons for not appreciating it. Try to solve her difficulty in the fewest possible removals with counters on a sheet of paper.

Here are seven pennies, all heads up. In a single move you can turn over any four of them. By repeatedly making such moves, can you eventually turn all seven pennies tails up?
Prove that, at any given moment, there are two points on the equator that are diametrically opposed yet have the same temperature.
Another puzzle from Henry Dudeney:
“It is a glorious game!” an enthusiast was heard to exclaim. “At the close of last season, of the footballers of my acquaintance, four had broken their left arm, five had broken their right arm, two had the right arm sound, and three had sound left arms.” Can you discover from that statement what is the smallest number of players that the speaker could be acquainted with?
From the 1977 all-Soviet-Union Mathematical Olympiad:
Seven dwarfs are sitting at a round table. Each has a cup, and some cups contain milk. Each dwarf in turn pours all his milk into the other six cups, dividing it equally among them. After the seventh dwarf has done this, they find that each cup again contains its initial quantity of milk. How much milk does each cup contain, if there were 42 ounces of milk altogether?