I have a 16-ounce bottle of wine and want to make it last as long as possible, so I establish the following plan: On the first day I’ll drink 1 ounce of wine and refill the bottle with water. On the second day I’ll drink 2 ounces of the mixture and refill the bottle with water. On the third day I’ll drink three ounces of the mixture and again refill the bottle with water. If I continue until the bottle is empty, how many ounces of water will I have drunk?
Puzzles
Weighty Matters
I’ve accidentally turned the calibration dial on my bathroom scale, so its readings are skewed by a consistent amount. Apart from that it works fine, though. When I stand on the scale it reads 170 pounds, when my wife stands on it it reads 130, and when we stand on it together it reads 292 pounds. How should I adjust the scale?
Black and White

From Alexander H. Robbins, A Collection of Chess Problems, 1887. White to mate in two moves.
Black and White
Waste Not …
A puzzle from Polish mathematician Paul Vaderlind:
John is swimming upstream in a river when he loses his goggles. He lets them go and continues upstream for 10 minutes, then decides to turn around and retrieve them. He catches up with them at a point one half mile from the point where he lost them. Is the river flowing faster than 1 mile per hour? (Assume that John swims at the same strength throughout.)
Twice Blessed

When Linus Pauling won his second Nobel Prize in 1962, he joked that receiving his second Nobel was less remarkable than receiving his first: The chance of anyone receiving his first Nobel Prize is one in several billion (the population of the world), while the chance of receiving his second is one in several hundred (the number of living people who have received one prize).
What’s wrong with this argument?
Side Issue
A conundrum by Russian puzzle maven Boris Kordemsky:
A work train composed of a locomotive and five cars has just stopped at a railway station when word comes that a passenger train is approaching. The smaller train must make way for it to pass through, but the station has only one siding, and this will accommodate only three cars (or an engine and two cars). How can it arrange to let the passenger train through?
Flying Fur

Sam Loyd devised this puzzle for P.T. Barnum:
A trained cat and dog run a race, one hundred feet straight away and return. The dog leaps three feet at each bound and the cat but two, but then she makes three leaps to his two. Now, under those circumstances, what are the possible outcomes of the race?
Lattice Work
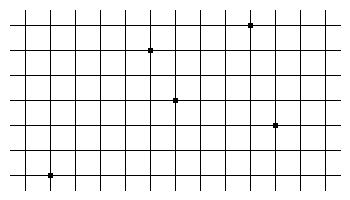
Plot five points at random at the intersections of a coordinate grid. Between each pair of points a line segment can be drawn. Prove that the midpoint of at least one of these segments occurs at an intersection of grid lines.
Black and White

By William Crane Jr., from the Sydney Town and Country Journal, 1877. White to mate in two moves.

