My doctor wants to establish a dosage for a new drug, so he gives me a bottle of 48 pills and tells me to take them throughout the month of June. I can take as many or as few as I like on any given day, so long as I take at least 1 pill each day. Show that there’s a sequence of consecutive days during which I take exactly 11 pills.
Puzzles
Readership
Assume that these statements are true:
- Not all Futility Closet readers are U.S. residents.
- All walrus veterinarians who are not U.S. residents are not Futility Closet readers.
- Not all Futility Closet readers are walrus veterinarians?
Do 1 and 2 imply that
Ones in a Million
Of the integers from 1 to 1,000,000, which are more numerous: the numbers that contain a 1 or those that don’t?
The Figure 8 Puzzle

Can this loop of string be freed from its wire? Stewart Coffin, who devised the puzzle in 1974, writes, “I soon became convinced that this was impossible, but being a novice in the field of topology, I was at a loss for any sort of formal proof.” He published the challenge in a newsletter and has been receiving requests for a solution ever since. Adding to the confusion, in 1976 a British puzzle editor mistakenly claimed with that Coffin’s creation was equivalent to another puzzle with a known solution, and Pieter van Delft and Jack Botermans published an amusingly bewildering “solution” of their own in their 1978 book Creative Puzzles of the World.
In the meantime, fans around the world have continued to experiment, and mathematicians Inta Bertuccioni and Paul Melvin have both offered proofs that the puzzle is unsolvable. “Whoever would have guessed that this little bent piece of scrap wire and loop of string would launch itself on an odyssey that would carry it around the world?” Coffin writes. “Will it mischievously rise again, perhaps disguised in another form, as topological puzzles so often do?”
Black and White
Odd and Even
A puzzle by Noboyuki Yoshigahara:
“An odd number plus an odd number makes an even number. An even number plus an odd number makes an odd number. An even number plus an even number is an even number. Right?”
“Yes.”
“An odd number times an odd number is an odd number. An even number times an odd number is an even number. Right?”
“Sure.”
“An even number times an even number is an odd number. Right?”
“Huh?”
“You don’t think so? An even number times an even number is an odd number.”
“Why?”
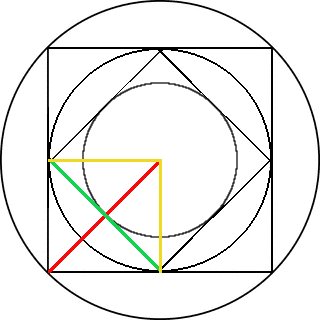
Circles and Squares
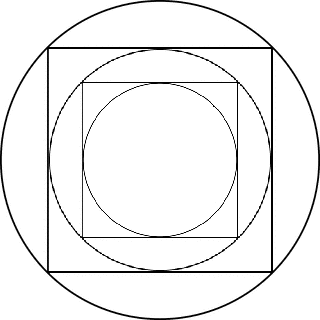
Here are three circles and two squares, inscribed successively as shown.
If the diameter of the largest circle is 10, what is the diameter of the smallest circle?
Heads of State
Ten senators are about to enter Congress when a barrage of snowballs knocks off their tophats. Each retrieves a hat at random. What is the probability that exactly nine of them receive their own hats?