
By Joseph Kling, from Chess Euclid, 1849. White to mate with the pawn in three moves.

By Joseph Kling, from Chess Euclid, 1849. White to mate with the pawn in three moves.
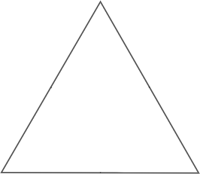
Five points are located in an equilateral triangle with 10-inch sides (or on its perimeter). What’s the maximum distance between the two closest points?
A magician invites me to do the following:
Now, after a period of mysterious activity under the table, he places his pack of 20 cards next to mine of 32. Using the dark arts, he says, he has arranged that both packs now contain the same number of face-up cards. We count, and they do. How has he accomplished this?

From Benjamin Glover Laws, The Two-Move Chess Problem, 1890. White to mate in two moves.
I have just moved to an island on which every intersection is the meeting of three two-way streets. On a lark I decide to go running, turning right at the first intersection, left at the next, and alternating in this way to decide my route. Prove that eventually I’ll return home.
I want to take my one-piece bass flute on the train, but it’s 1.7 meters long and the baggage man won’t take any item whose greatest dimension exceeds 1 meter. What can I do?
A man has two girlfriends, one who lives uptown and the other downtown. He likes them equally, so he lets the trains decide which he will visit: He arrives at the train station at random times and takes whichever train arrives first.
Over time, he finds that he’s visiting the uptown girlfriend much more often than the downtown girlfriend, even though uptown and downtown trains arrive at the station equally often. Why?
An odd number of people armed with water guns are standing in a field so that all the pairwise distances are distinct. At a signal, each shoots at his nearest neighbor and hits him. Prove that one person doesn’t get wet.
On a multiple-choice test, one of the questions is illegible, but the choice of answers is listed clearly below. What’s the right answer?
(a) All of the below.
(b) None of the below.
(c) All of the above.
(d) One of the above.
(e) None of the above.
(f) None of the above.