A problem from the January-February 1991 issue of Quantum:
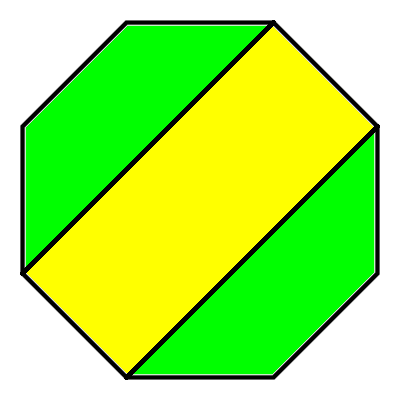
Prove that the area of the yellow rectangle is half that of the full octagon.
A problem from the January-February 1991 issue of Quantum:

Prove that the area of the yellow rectangle is half that of the full octagon.

Thomas Taverner published this remarkable problem in the Dubuque Chess Journal in 1889. White is to mate in two moves.
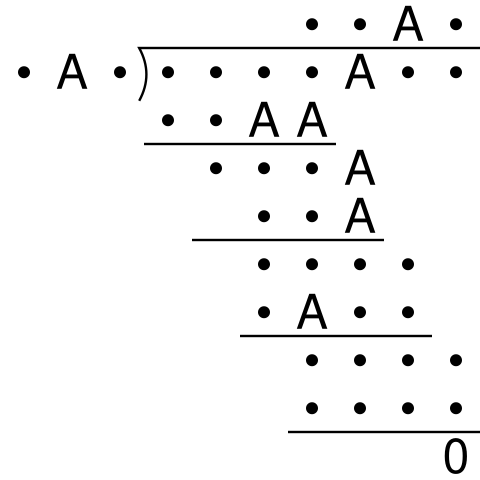
Writing home from Princeton in 1939, 21-year-old Richard Feynman challenged his father to solve “this problem in long division. Each of the dots represents some digit (any digit). Each of the A’s represent the same digit (for example, a 3). None of the dots are the same as the A (i.e., no dot can be a 3 if A is 3).”
We don’t know whether his father succeeded — the solution is quite involved:
Two sadistically addressed letters, from the Strand, August 1897:
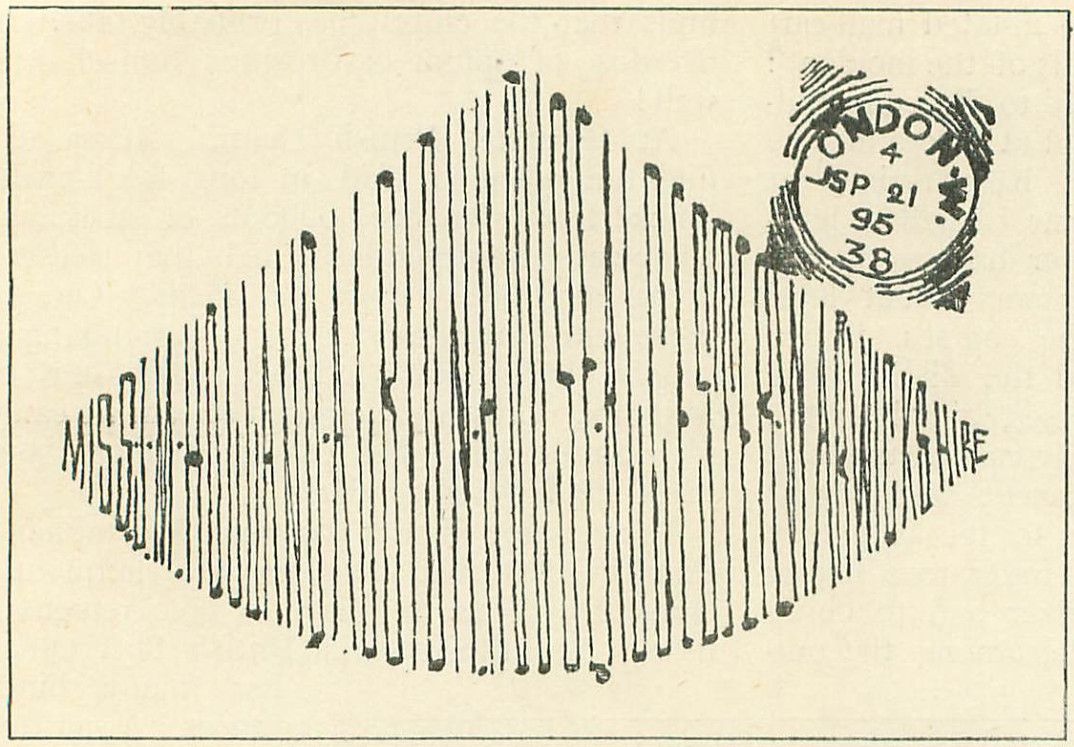
“The accompanying envelope looks hopeless at first glance. It is a fair sample of the kind of thing which is specially invented to try the patience of the splendid staff of officials at the G.P.O. Hold it horizontally, on a level with the eyes, and you will read the address: ‘Miss J. M. Holland, Albion House, Alcester, Warwickshire.'”
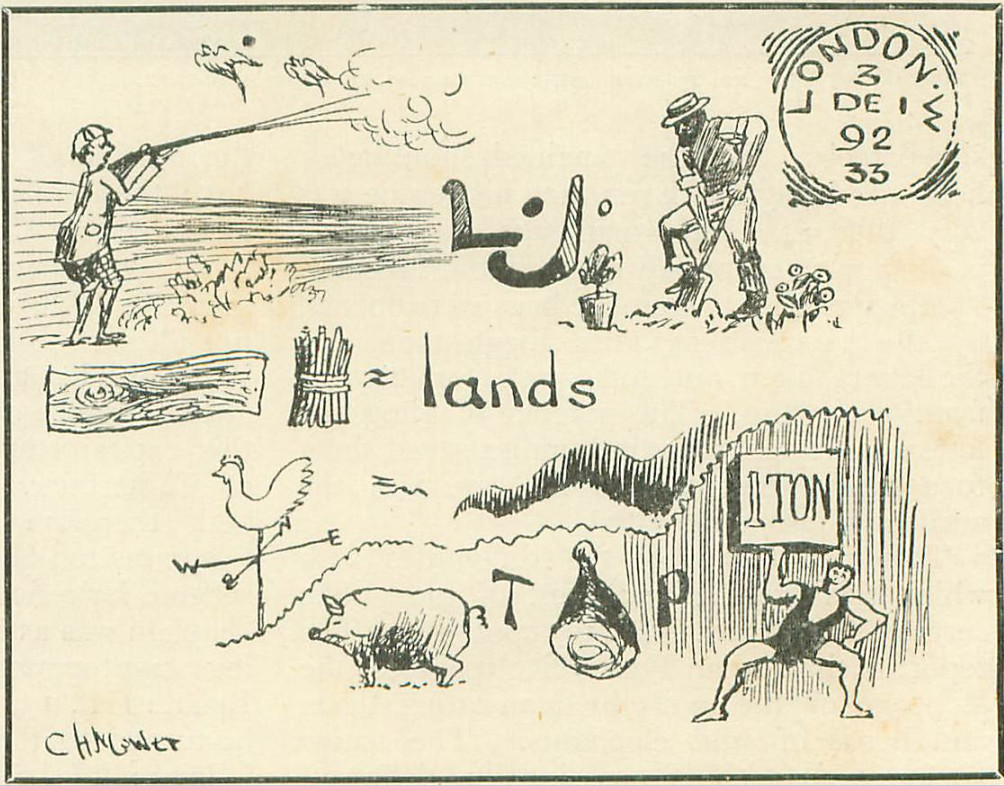
“The next reproduction, specially photographed from the Curious Address Books at the G.P.O. Museum, is even more typical of mis-directed ingenuity. This is a picture-puzzle, the address being: ‘Miss L.J. Gardner, Woodlands, West End, Southampton.'”
Three girls dressed up in white, green, and blue dresses. They also wore shoes of these three colors. Only Ann wore a dress of the same color as her shoes. Neither Betty’s dress nor her shoes were white, and Carol’s shoes were green. What was the color of each girl’s dress?
Four people are traveling in the dark when they arrive at a river. The narrow bridge can accommodate only two people at a time, and the group has only one torch, which must accompany each party that makes a crossing. Persons A, B, C, and D can cross in 1, 2, 5, and 8 minutes, respectively, and any pair of travelers can move only at the pace of the slower person. The torch will go out in 15 minutes. Can they all get safely across?
A puzzle by Jared Z., Nicole H., and Benjamin E., mathematicians at the National Security Agency:
The chief detective hurried down to the police station after hearing big news: there was a heist at Pi National Bank! The police had brought in seven known gang members seen leaving the scene of the crime. They belonged to the nefarious True/False Gang, so named because each member is either required to always tell the truth or required to always lie, although everyone is capable of engaging in wrongdoing. The chief also knew from his past cases that any crime committed by the gang always included one truth teller.
When the chief showed up, he asked the gang members the following questions:
1) Are you guilty?
2) How many of the seven of you are guilty?
3) How many of the seven of you tell the truth?
Here were their responses:
Person 1: Yes; 1; 1
Person 2: Yes; 3; 3
Person 3: No; 2; 2
Person 4: No; 4; 1
Person 5: No; 3; 3
Person 6: No; 3; 3
Person 7: Yes; 2; 2
After looking these answers over, the chief prepared to arrest those responsible.
Which of these seven did the chief arrest?
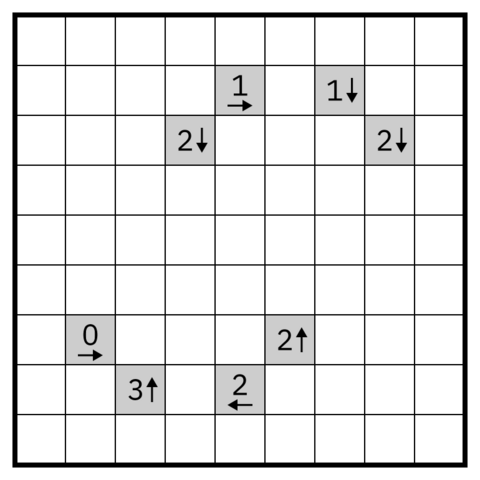
The goal of this logic puzzle is simple: to draw an orthogonally connected, non-intersecting loop that passes through every white square on the board. The trouble is that the board contains some number of black squares, and these are hidden. The only clues to their location are the numbers in the gray squares. In the diagram above, there are exactly 3 black squares in the third file north of the “3” indicator. And there are no black squares on the third rank anywhere east of the “0” indicator.
Gray squares can’t be black, no two black squares are orthogonally adjacent, and there may be some black squares that aren’t referred to by any of the indicators.
Knowing all this (and knowing that a solution is possible), can you determine the location of all the black squares and draw a loop that passes through all the white ones?

A logic problem in the shape of a chess puzzle, by Éric Angelini. White has just moved. What was his move?