
A poser from Jerome S. Meyer’s Puzzle Quiz and Stunt Fun (1956):
“The mark above is the mark of evil. It is the symbol of murder and terror. Millions have died for it and millions have died because of it. Can you tell what it is?”

A poser from Jerome S. Meyer’s Puzzle Quiz and Stunt Fun (1956):
“The mark above is the mark of evil. It is the symbol of murder and terror. Millions have died for it and millions have died because of it. Can you tell what it is?”
Twenty-five basketball teams compete in a knockout tournament — each team is eliminated after its first loss. How many games must be played to establish a winner?
1. P-K4 P-K4 2. B-B4 P-R4 3. Q-B3 P-R4 4. QxP mate:

That’s a pretty colorless chess game, but Mike Keith points out that the game score makes an alphametic:
P-K4 + P-K4 + B-B4 + P-R4 + Q-B3 + P-R4 + QxP = IWIN
Replace each letter and symbol (-, x) with a digit, leaving the numbers as they are, to produce a valid equation.
1. You are midway through dealing a bridge hand when a nuclear apocalypse destroys civilization. The bridge table is still upright, and your friends are willing to keep playing, but you can’t remember where you left off dealing. How can you finish dealing this hand without having to start over?
2. Can I stand behind you while you stand behind me?
3. My bed is 10 feet from the light switch. But last week I turned off the light, dashed across the room, and was in bed before the room got dark. How did I manage this?
A puzzle by Henry Dudeney:
A robber broke into the belfry of a church, and though he had nothing to assist him but his pocket-knife, he contrived to steal nearly the complete lengths of the two bell-ropes, which passed through holes in the lofty boarded ceiling. How did he effect his purpose? Of course, there was no ladder or aught else to assist him. It is easy to understand that he might steal one rope and slide down the other, but how he cut the two, or any considerable portion of them, without a bad fall, is perplexing.
In a chess game, White plays 1. f3 2. Kf2 3. Kg3 4. Kh4. Black’s fourth move checkmates White. What is the game?
1. f3 e5 2. Kf2 Qf6 3. Kg3 Qxf3+! 4. Kh4 Be7#

White’s play is so suicidal that the task sounds easy, but “this problem is almost impossibly difficult because Qxf3+ is such a horrible move by normal chess standards,” writes former U.S. champion Stuart Rachels. “It is hard for a competent player to consciously consider it.”
Here’s another problem by Sam Loyd:

White to mate in two moves. In 1907 J.H. Blackburne chose this as one of his all-time favorite problems. “It was first published in this country about fifty years ago, and greatly puzzled the solvers of that day, the idea then being entirely new.”
It’s a perfectly fair two-mover — there’s no trickery.
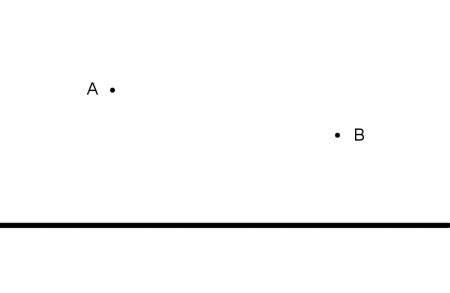
A gold miner lives at point A, 3 miles north of the river and 5 miles upstream from the gold mine at point B, which is 2 miles north of the river. On the way to work he must stop at the river to give his burro a drink. At what point on the river should he stop in order to minimize the length of the trip?

The American Chess Bulletin of October 1917 contains a puzzle story about a boastful player who entered a local club claiming to have beaten one of the best players in the county.
Our first question was: ‘What odds did he give you?’
‘Why, none, of course,’ was the reply. ‘Topnotch was White, and he set up a fierce King’s side attack on my castled K. I had almost given up all hope when I saw that if I could only get my Kt to QR5, and he went on with his attack, I had a mate. So on my 15th move I played Kt-QR5. As I hoped, he overlooked the mate which he could have stopped with a move, and played 16 Kt-KR5, and then, of course, I mated. That is the position.’
And he set it up with the air of a conqueror.
We looked at it, saw the mate (a very commonplace one, by the way), and were turning away, when the Problemist, who was the most ‘fed up’ of us all, said in his quietest voice:
‘S—, you are a beautiful–Ananias.’
We started in surprise; it was so unlike him.
S—, with a red face and heated manner, said: ‘What do you mean? I give you my word of honor that was the position after White’s 16th move.’
‘I don’t dispute it; but still you are not telling the truth.’ And he proceeded to demonstrate to our satisfaction he was right.
During this period S— disappeared and I think it unlikely that we shall receive another visit from him.
Now, what did the Problemist demonstrate?
“Can our solvers unravel this mystery?” wrote the editors. “It is plain that the Problemist synthetically deduced that by no possibility could S— have met this precise position in the course of orthodox chess play.”
Alas, I don’t have the solution! If S— is telling the truth, then in the diagram above the black knight must have moved from b6 and the white knight from f4. Black’s mate would have been something like 16. … Nc3+ 17. bxc3 Qb6+ 18. cxb6 Rxb6+ 19. Ka1 Bxc3#. But none of these observations seems to lead anywhere. Any ideas?
UPDATE: A number of readers have analyzed this, and the strong consensus is that the position above cannot have been reached in 16 moves, as S— says it did. I had dismissed this possibility when the Problemist said “I don’t dispute it,” thinking this meant he accepted S—‘s contended move totals, but now I think that remark meant merely that the Problemist thinks S— generally dishonest. Thanks to everyone who saw more deeply than I did.
SECOND UPDATE: Wait. Another reader points out that perhaps the idea is that White’s position can be reached in 16 moves — if he gave knight odds. This is much more satisfying — the Problemist isn’t disputing the number of moves; he’s pointing out that Topnotch had offered to play with a significant handicap. This would embarrass the boastful S—, giving the whole story a satisfying punchline. It also explains why S— is asked explicitly about odds at the start, and it illuminates the rather canny phrasing about “orthodox” chess play. I’ll bet this is it.

A classroom contains 25 desks arranged in 5 rows and 5 columns. The teacher asks each student to move to the desk in front of, behind, to the left of, or to the right of her current desk. The students at the edges have limited choices — will every child be able to find a new seat?