Like Nabokov, Lord Dunsany was fond of composing chess problems. This example was published in Hubert Phillips’ Week-end Problems Book of 1932:

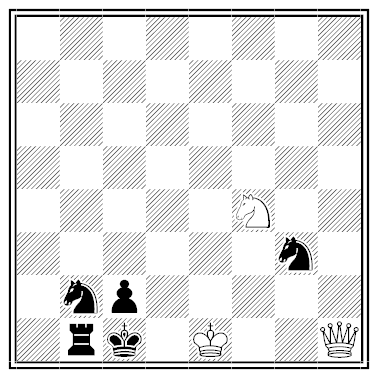
Two eccentric gentlemen abandoned this position at a chess club — White had announced mate in four. What was the mate?
The key is to notice that Black’s king and queen have changed positions. This is not possible if the black pawns are on their home squares. And this means that we’ve been viewing the position upside down:

Now it’s clear that Black is hemmed in by his own pawns — White can mate him in four moves with the b8 knight, e.g. by 1. Nc6 Nf3 2. Nb4 (threatening Nd3#) Ne5 3. Qxe5 (any) 4. Nd3#.
Dunsany drew a game against Capablanca in a simultaneous exhibition in London in April 1929. He later wrote:
One art they say is of no use;
The mellow evenings spent at chess,
The thrill, the triumph, and the truce
To every care, are valueless.
And yet, if all whose hopes were set
On harming man played chess instead,
We should have cities standing yet
Which now are dust upon the dead.