
By Sam Loyd. In how few moves can White force Black to mate him?
The answer is to castle queenside:

Now every Black move is mate.

By Sam Loyd. In how few moves can White force Black to mate him?
The answer is to castle queenside:

Now every Black move is mate.
Each point in an infinite plane is colored either red or blue. Prove that there are two points of the same color that are exactly 1 meter apart.

The Schachfreund, edited by M. Alapin, gives the following amusing Chess Skit. A well-known chess master allowed weak opponents to make as many moves as they pleased during five minutes, as odds, before the beginning of a game, with the provision that they confined their moves to their own half of the board. At the end of the five minutes the game commenced, the odds-giver having the first move. During the five minutes one of them had played: [1. a4 2. Na3 3. h4 4. Nf3 5. d4 6. Nd2 7. Rh3 8. Nac4 9. Raa3 10. Ne4 11. Qd2 12. Rhf3 13. g3 14. Bh3 15. Qf4 16. Rae3], whereupon the odds-giver resigned without having made a single move, as he could not avoid mate in two.
— The British Chess Magazine, January 1899
In the 1890s an eminent Scot began to publish short popular science articles under an assumed name, for “the fun of seeing if he [could] make another reputation for himself.”
He succeeded, publishing three articles in the National Geographic before the secret leaked out.
The pseudonym was H.A. Largelamb. Who was the man?
A calisson is a flat French candy traditionally manufactured in the shape of two equilateral triangles joined along an edge. Suppose a quantity of these are packed randomly into a hexagonal container:
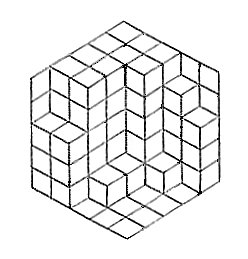
Each candy must take one of three orientations: east-west, northeast-southwest, or northwest-southeast.
As it happens, no matter how the candies are packed into the hexagon, an equal number will take each of these three orientations.
In the May 1989 issue of the American Mathematical Monthly, Guy David and Carlos Tomei demonstrated this with a beautifully intuitive “proof without words.” What had they seen?

You’re in a pitch-dark room. On a table before you are 12 pennies. You know that 5 are heads up and 7 are tails up, but you don’t know which are which. By moving and flipping the coins you must produce two piles with an equal number of heads in each pile. How can you do this without seeing the coins?
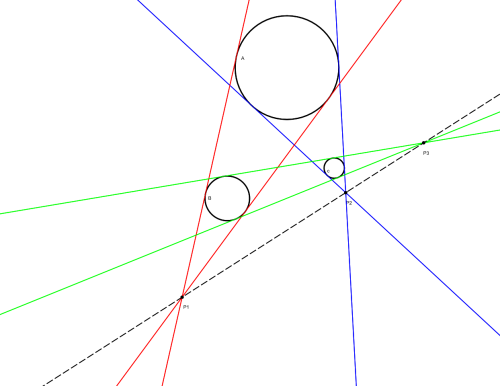
Draw three nonintersecting circles of different sizes, and bracket each pair of them with tangents. Each pair of tangents will intersect in a point, and these three points will always lie along a line.
On being shown this theorem, Cornell engineering professor John Edson Sweet paused and said, “Yes, that is perfectly self-evident.” What intuitive proof had he seen?
Literary critic A.N. Wilson panned Bevis Hillier’s 1988 biography of John Betjeman. To get even, Hillier forged a love letter ostensibly written by Betjeman in 1944 and forwarded it to Wilson under the name Eve de Harben (an anagram for “Ever been had?”). Wilson took the bait and included the forged letter in his own biography of Betjeman, which was published in 2005.
Here’s the letter. It contains a hidden message — can you find it?
Darling Honor,
I loved yesterday. All day, I’ve thought of nothing else. No other love I’ve had means so much. Was it just an aberration on your part, or will you meet me at Mrs Holmes’s again — say on Saturday? I won’t be able to sleep until I have your answer.
Love has given me a miss for so long, and now this miracle has happened. Sex is a part of it, of course, but I have a Romaunt of the Rose feeling about it too. On Saturday we could have lunch at Fortt’s, then go back to Mrs. H’s. Never mind if you can’t make it then. I am free on Sunday too or Sunday week. Signal me tomorrow as to whether and when you can come.
Anthony Powell has written to me, and mentions you admiringly. Some of his comments about the Army are v funny. He’s somebody I’d like to know better when the war is over. I find his letters funnier than his books. Tinkerty-tonk, my darling. I pray I’ll hear from you tomorrow. If I don’t I’ll visit your office in a fake beard.
All love, JB
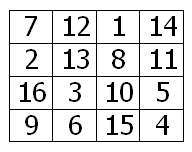
Roll this magic square into a tube by joining the upper and lower edges, then join the ends of the tube. Every row, column, and diagonal on the resulting torus will add to 34.
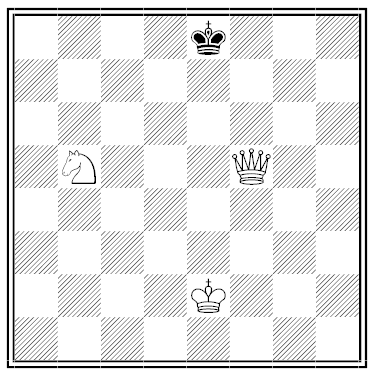
Bend this chessboard similarly into a torus, then mate in 4.
Hint: The solution comprises only two lines.

From Clark Kinnaird’s Encyclopedia of Puzzles and Pastimes, 1946:
Though a great American, Wendell Willkie nevertheless lacked one of the four necessary requirements for becoming President of the United States. One must be at least 35, a native-born American, and a resident of the U.S.A. for at least 14 years. Name the fourth requirement which Willkie also lacked?