A favorite problem of Lewis Carroll involves a customer trying to complete a purchase using pre-decimal currency. He wants to buy 7s. 3d. worth of goods, but he has only a half-sovereign (10s.), a florin (2s.), and a sixpence. The shopkeeper can’t give him change, as he himself has only a crown (5s.), a shilling, and a penny. As they’re puzzling over this a friend enters the shop with a double-florin (4s.), a half-crown (2s. 6d.), a fourpenny-bit, and a threepenny-bit. Can the three of them negotiate the transaction?
Happily, they can. They pool their money on the counter, and the shopkeeper takes the half-sovereign, the sixpence, the half-crown, and the fourpenny-bit; the customer takes the double-florin, the shilling, and threepenny-bit as change; and the friend takes the florin, the crown, and the penny.
“There are other combinations,” writes John Fisher in The Magic of Lewis Carroll, “but this is the most logistically pleasing, as it will be seen that not one of the three persons retains any one of his own coins.”
Related: From Henry Dudeney, a magic square:
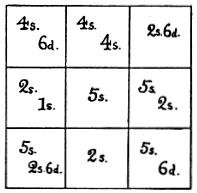
(Strand, December 1896)