By T.R. Dowson. White to mate in 21 moves:
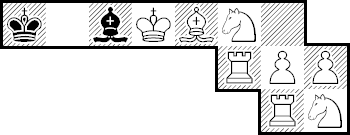
It’s not as hard as it sounds, though it’s a bit like a square dance in a submarine.
By T.R. Dowson. White to mate in 21 moves:

It’s not as hard as it sounds, though it’s a bit like a square dance in a submarine.
In a certain library, no two books contain the same number of words, and the total number of books is greater than number of words in the largest book.
How many words does one of the books contain, and what is it about?
At 1:17 one afternoon a canoeist left his riverside camp and paddled upstream at 4 mph against a current of 1.5 mph. At 2:05 he passed a corked bottle floating downstream and noticed that it contained a message. He paddled some distance further but finally couldn’t help himself — he turned around and paddled after the bottle. He caught it just as it reached his camp. The message read:
HOW FAR DID YOU GET FROM CAMP BEFORE YOU GAVE IN TO YOUR CURIOSITY?
“There is no reason why the camper should have paid any attention to this odd message, but you know how these things are,” writes Geoffrey Mott-Smith in Mathematical Puzzles for Beginners and Enthusiasts (1946). The camper had noticed a landmark at the point upstream where he’d turned around, so he was able to measure the distance the next day. But he could have reasoned the thing out from the facts. Can you?
Prove that the number of people who shake hands an odd number of times at the opera next Thursday will be even.
From Henry Dudeney:
Two men are seated at a square-topped table. One places an ordinary cigar (flat at one end, pointed at the other) on the table, then the other does the same, and so on alternately, a condition being that no cigar shall touch another. Which player should succeed in placing the last cigar, assuming that they each will play in the best possible manner? The size of the table top and the size of the cigar are not given, but in order to exclude the ridiculous answer that the table might be so diminutive as only to take one cigar, we will say that the table must not be less than 2 feet square and the cigar not more than 4-1/2 inches long. With those restrictions you may take any dimensions you like. Of course we assume that all the cigars are exactly alike in every respect. Should the first player, or the second player, win?
Geoffrey Mott-Smith writes, “I cannot resist narrating that I first became acquainted with this gem while reading in bed, and that like an illustrious precursor I startled the household by jumping out of bed, dancing about crying ‘Eureka! Eureka!'”
What had he seen?

You have 100 pounds of Martian potatoes, which are 99 percent water by weight. You let them dehydrate until they’re 98 percent water. How much do they weigh now?

Zachary challenges his brother Alexander to a 100-meter race. Alexander crosses the finish line when Zachary has covered only 97 meters.
The two agree to a second race, and this time Alexander starts 3 meters behind the starting line.
If both brothers run at the same speed as in the first race, who will win?
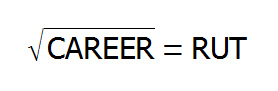
A depressing alphametic by Joseph Madachy. Each letter stands for a digit. What are the digits?