Solution:
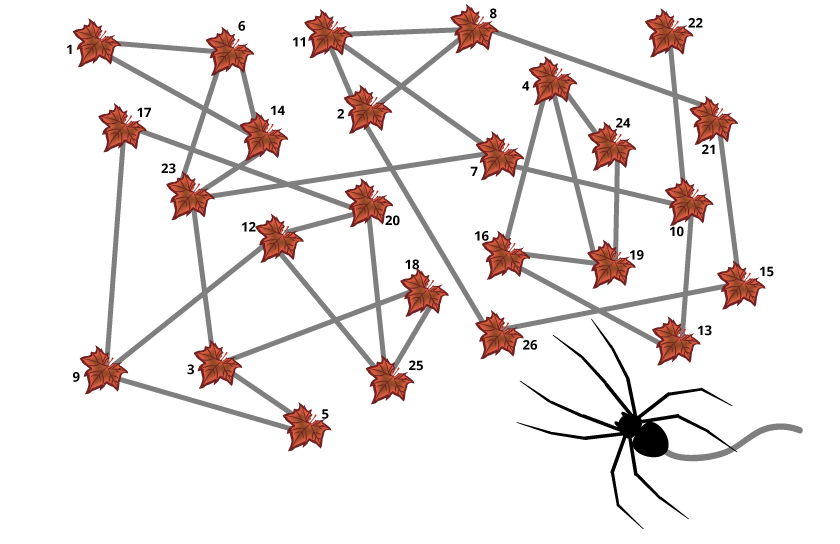
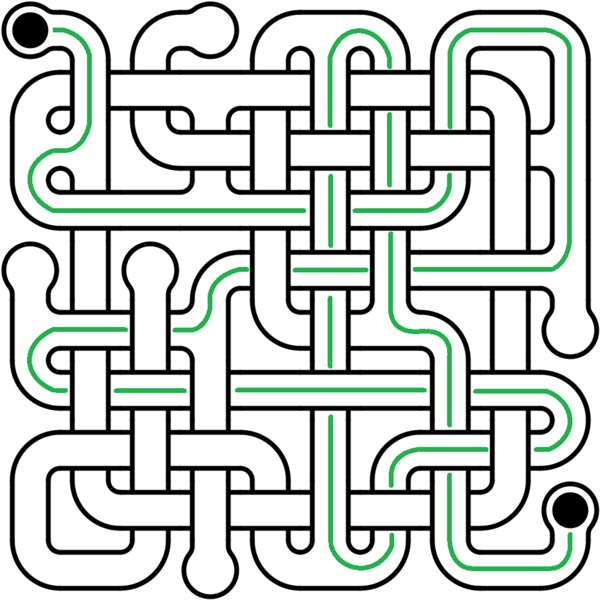
This problem has 4 solutions and answers: 5-13, 5-22, 18-13, 18-22. Only the first solution is fully drawn on the solution illustration, but all four are explained below.
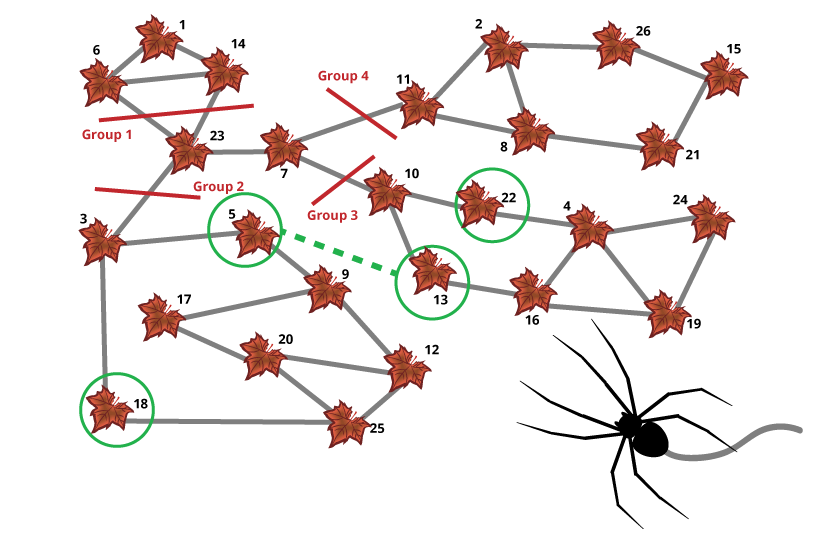
Explanation:
First, let’s re-draw the situation to be less messy! Once we’ve organized the leaves a bit, we see that there are 4 distinct groups of leaves which can only be accessed via one leaf: Group 1 is only accessible via leaf 23, Group 2 via leaf 3, Group 3 via leaf 10, and Group 4 via leaf 11.
Here we see the problem — once Arabella has entered a group of leaves, she cannot get out again without crossing the ‘access leaf’ again. For Group 1 this is okay, since Arabella can start on leaf 1, move to leaf 6, then leaf 14, then exit at leaf 23, and doesn’t need to go back in. Similarly, Group 4 contains the last leaf, so Arabella can enter the group from leaf 11, then go to leaf 2, leaf 8, leaf 21, leaf 15, and exit at leaf 26.
But for Group 2 and Group 3, Arabella must enter and exit the group. This is where the extra web comes in handy! If we connect a leaf in Group 2 and a leaf in Group 3, then Arabella can go from Group 1 to Group 2 using leaf 23, then Group 2 to Group 3 using the new web, and finally from Group 3 to Group 4 using leaf 7.
However, not just any leaves from Group 2 and Group 3 will work. Arabella must cover all of Group 2 before moving to Group 3, and cover all of Group 3 before going to Group 4. This still allows for a few different combinations: from Group 2 we can use leaf 5 or leaf 18; from Group 3 we can use leaf 13 or leaf 22.
Here are the different paths Arabella could take for each combination (there are minor variations in all of the paths, such as switching the order of leaves 6 and 14, which are unaffected by the solution choice, but we will not list those):
- Leaves 5 & 13 — 1, 6, 14, 23, 3, 18, 25, 12, 20, 17, 9, 5, 13, 16, 19, 24, 4, 22, 10, 7, 11, 2, 8, 21, 15, 26
- Leaves 5 & 22 — 1, 6, 14, 23, 3, 18, 25, 12, 20, 17, 9, 5, 22, 4, 24, 19, 16, 13, 10, 7, 11, 2, 8, 21, 15, 26
|