How many pets do I have if all of them are dogs except two, all are cats except two, and all are fish except two?
Puzzles
“Four Puzzles in One”
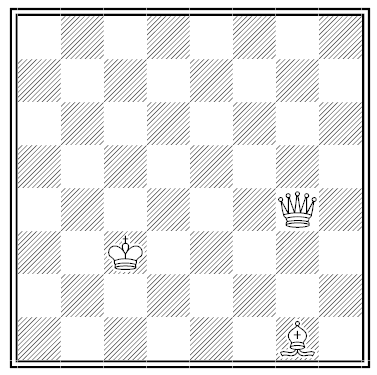
By Sam Loyd. Place the black king (a) where it can be checkmated on the move, (b) where it’s in stalemate, (c) where it’s in checkmate, and (d) where the three white pieces can’t be arranged to checkmate it.
Mate in Two

By G.A.A. Walker. White to play and checkmate all six black kings simultaneously with his second move.
A Mysterious Windfall
A riddle by Isaac Newton:
Four people sat down at a table to play;
They play’d all that night, and some part of next day;
This one thing observ’d, that when all were seated,
Nobody play’d with them, and nobody betted;
Yet, when they got up, each was winner a guinea;
Who tells me this riddle I’m sure is no ninny.
Who are the players?
Erin Go
Count these leprechauns:

Now swap the two upper panels and count again:

Where has the extra one been hiding?
Hidden in Sight
This puzzling verse, from a contributor named “Maude,” appeared in the Weekly Wisconsin of Sept. 29, 1888:
Perhaps the solvers are inclined to hiss,
Curling their nose up at a con like this.
Like some much abler posers I would try
A rare, uncommon puzzle to supply.
A curious acrostic here you see
Rough hewn and inartistic tho’ it be;
Still it is well to have it understood,
I could not make it plainer, if I would.
(In the second line, “con” means “contribution.”)
What are the concealed words?
Cornered
One of Eduard Gufeld’s first chess coaches, A.A. Olshansky, offered him this problem:
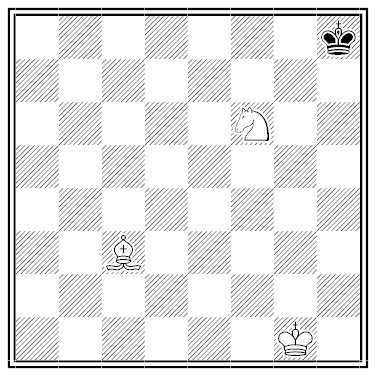
“White to mate in half a move.”
A Curious Exchange
Census Taker: How old are your three daughters?
Mrs. Smith: The product of their ages is 36, and the sum of their ages is the address on our door here.
Census Taker: (after some figuring) I’m afraid I can’t determine their ages from that …
Mrs. Smith: My eldest daughter has red hair.
Census Taker: Oh, thanks, now I know.
How old are the three girls?
The Canals on Mars

From Sam Loyd:
Here is a map of the newly discovered cities and waterways on our nearest neighbor planet, Mars. Start at the city marked T, at the south pole, and see if you can spell a complete English sentence by making a tour of all the cities, visiting each city only once, and returning to the starting point.
When this puzzle originally appeared in a magazine, more than fifty thousand readers reported, ‘There is no possible way.’ Yet it is a very simple puzzle.
I’ll withhold the answer.
Equal Time

A puzzle from Russia:
Draw two straight lines on the clock face so that the sums of the numbers in each part are equal.


