At a Cambridge dinner, Arthur C. Clarke asked Clive Sinclair, “What was the first human artifact to break the sound barrier?”
What was it?
At a Cambridge dinner, Arthur C. Clarke asked Clive Sinclair, “What was the first human artifact to break the sound barrier?”
What was it?
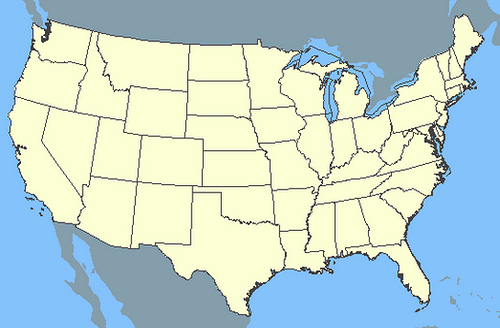
John lives in an East Coast state and Mary in a West Coast state. During a phone conversation one night, they realize that it is the same time in both locations. How can this be?
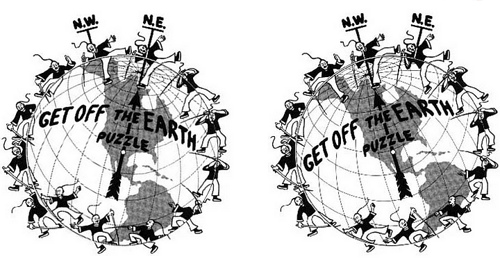
Patented in 1896, Sam Loyd’s “Get Off the Earth” puzzle reportedly sold more than 10 million copies during the puzzlemaker’s lifetime, making it one of the most popular puzzles of all time.
There are 13 men in the figure on the left. Rotating the earth produces the figure on the right — which has 12 men. What happened to the 13th man?
A man drives 1 mile to the top of a hill at 15 mph. How fast must he drive 1 mile down the other side to average 30 mph for the 2-mile trip?
You hate visiting your girlfriend because there’s no elevator in her apartment building. And now she’s moved from the fourth floor to the seventh. How many times longer does this make your ascent?
Many masculine nouns can be converted to feminine with a suffix, as HERO-HEROINE and HOST-HOSTESS.
Name a feminine noun that can be converted to masculine with a suffix.

Every room in my house has an even number of doors.
Prove that the house has an even number of exterior doors.
One train leaves Los Angeles for New York at 60 mph.
At the same time, another train leaves New York for Los Angeles at 40 mph.
What is the distance between them one hour before they meet?
A.A. Bennett offered this puzzle in the American Mathematical Monthly of May 1937:
A car with n (n > 2) passengers of different speeds of mental reaction passes through a tunnel and each passenger acquires unconsciously a smudge of soot upon his forehead. Suppose that each passenger
(1) laughs and continues to laugh as soon as and only so long as he sees a smudge upon the forehead of a fellow passenger;
(2) can see the foreheads of all his fellows;
(3) reasons correctly;
(4) will clean his own forehead when and only when his reasoning forces him to conclude that he has a smudge;
(5) knows that (1), (2), (3), and (4) hold for each of his fellows.
Show that each passenger will eventually wipe his own forehead.