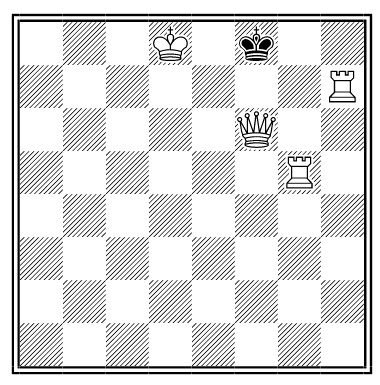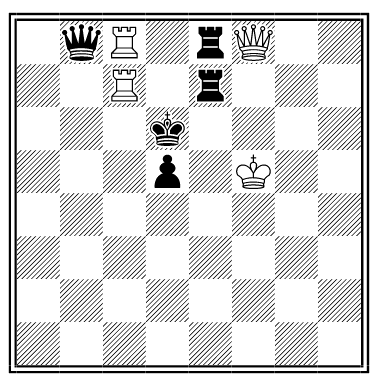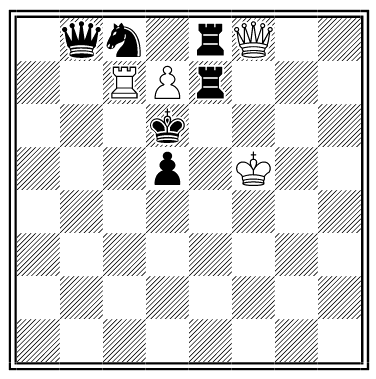
By J. Kling. White to mate in 64 moves, forcing the black king to occupy every square on the board:
1. Rb8+ Ka7 2. Qc7+ Ka6 3. Qb7+ Ka5 4. Qb6+ Ka4 5. Rc4+ Ka3 6. Qe3+ Ka2 7. Rc2+ Ka1 8. Ra8+ Kb1 9. Rcc8 Kb2 10. Qc1+ Kb3 11. Ra3+ Kb4 12. Qc3+ Kb5 13. Rc5+ Kb6 14. Qa5+ Kb7 15. Rd3 Kb8 16. Rb5+ Kc8 17. Qa8+ Kc7 18. Qb8+ Kc6 19. Rb6+ Kc5 20. Qd6+ Kc4 21. Rd4+ Kc3 22. Qb4+ Kc2 23. Re6 Kc1 24. Rc4+ Kd1 25. Qb1+ Kd2 26. Qc1+ Kd3 27. Rc3+ Kd4 28. Qe3+ Kd5 29. Re5+ Kd6 30. Qc5+ Kd7 31. Rf3 Kd8 32. Rd5+ Ke8 33. Qc8+ Ke7 34. Qd8+ Ke6 35. Rd6+ Ke5 36. Rf7 Ke4 37. Qf6 Ke3 38. Qd4+ Ke2 39. Rh6 Ke1 40. Re7+ Kf1 41. Qg7 Kf2 42. Rh1 Kf3 43. Qg1 Kf4 44. Qg2 Kf5 45. Qg3 Kf6 46. Qe5+ Kg6 47. Qe6+ Kg5 48. Qf7 Kg4 49. Rh5 Kg3 50. Qf5 Kg2 51. Qf4 Kg1 52. Rg5+ Kh1 53. Qe4+ Kh2 54. Kf7 Kh3 55. Qg2+ Kh4 56. Rg4+ Kh5 57. Re5+ Kh6 58. Qc6+ Kh7 59. Ke8 Kh8 60. Rh4+ Kg7 61. Kd8 Kg8 62. Rg5+ Kf7 63. Rh7+ Kf8 64. Qf6#