Donald Aucamp offered this problem in the Puzzle Corner department of MIT Technology Review in October 2003. Three logicians, A, B, and C, are wearing hats. Each of them knows that a positive integer has been painted on each of the hats, and each of them can see her companions’ integers but not her own. They also know that one of the integers is the sum of the other two. Now they engage in a contest to see which can be the first to determine her own number. A goes first, then B, then C, and so on in a circle until someone correctly names her number. In the first round, all three of them pass, but in the second round A correctly announces that her number is 50. How did she know this, and what were the other numbers?
Puzzles
“Pythagoras’ Classical Problem”
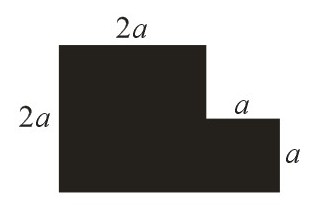
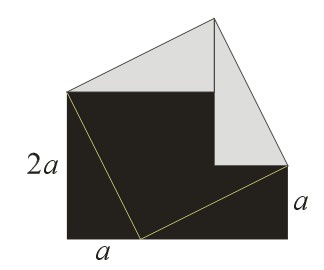
A pretty dissection puzzle by Sam Loyd. Cut this figure into three pieces that will fit together to make a square.
Card Algebra
From Henry Dudeney:
Take an ordinary pack of playing cards and regard all the court cards as tens. Now, look at the top card — say it is a seven — place it on the table face downwards and play more cards on top of it, counting up to twelve. Thus, the bottom card being seven, the next will be eight, the next nine, and so on, making six cards in that pile. Then look again at the top card of the pack — say it is a queen — then count 10, 11, 12 (three cards in all), and complete the second pile. Continue this, always counting up to twelve, and if at last you have not sufficient cards to complete a pile, put these apart. Now, if I am told how many piles have been made and how many unused cards remain over, I can at once tell you the sum of all the bottom cards in the piles. I simply multiply by 13 the number of piles less 4, and add the number of cards left over. Thus, if there were 6 piles and 5 cards over, then 13 times 2 (i.e. 6 less 4) added to 5 equals 31, the sum of the bottom cards. Why is this?
Self-Reference
A problem from the October 1959 issue of Eureka, the journal of the Cambridge University Mathematical Society:
A. The total number of true statements in this problem is 0 or 1 or 3.
B. The total number of true statements in this problem is 1 or 2 or 3.
C. The total number of true statements in this problem (excluding this one) is 0 or 1 or 3.
D. The total number of true statements in this problem (excluding this one) is 1 or 2 or 3.
Which of these statements are true?
Coming and Going
Two runners start from the same point on a circular track and run at different constant speeds. If they run in opposite directions on the track, they meet after a minute. If they run in the same direction, they meet after an hour. What’s the ratio of their speeds?
Economy
In an office the boy owed one of the clerks threepence, the clerk owed the cashier twopence, and the cashier owed the boy twopence. One day the boy, having a penny, decided to diminish his debt, and gave the penny to the clerk, who in turn paid half his debt by giving it to the cashier, the latter gave it back to the boy, saying, ‘That makes one penny I owe you now;’ the office boy again passed it to the clerk, who passed it to the cashier, who in turn passed it back to the boy, and the boy discharged his entire debt by handing it over to the clerk, thereby squaring all accounts.
— John Scott, The Puzzle King, 1899
RSS Quiz
The Royal Statistical Society’s Christmas Quiz runs through January 29 this year — 18 fiendish puzzles to mark the tradition’s 30th anniversary.
“Cracking the puzzles below will require a potent mix of general knowledge, logic, lateral thinking and searching skills — but, as usual, no specialist mathematical knowledge is needed.”
Entry is free and open to everyone. The top two entries will receive £100 and £50 in gift vouchers of their choice, and the quizmaster has pledged a donation of £900 to charities nominated by the top performers.
See the quiz web page for rules, entry instructions, and some tips for budding solvers.
Time’s Up
A perplexing question by the Soviet science writer Yakov Perelman:
If a clock takes three seconds to strike three, how long does it take to strike seven?
Relative

A problem from the October 1962 issue of Eureka, the journal of the Cambridge University Mathematical Society:
Tom is twice as old as Dick was when Tom was half as old as Dick will be when Tom is twice as old as Dick was when Tom was a year younger than Dick is now. Dick is twice as old as Tom was when Dick was half as old as Tom was when Dick was half as old as Tom was two years ago. How old are Dick and Tom?
Working Out
A problem by Polish mathematician Paul Vaderlind:
Each child in a school plays either tennis or soccer. One-ninth of the tennis players also play soccer, and one-seventh of the soccer players also play tennis. Do more than half the children play tennis?