Profile

A problem from the Stanford University Competitive Examination in Mathematics:

How old is the captain, how many children has he, and how long is his boat? Given the product 32118 of the three desired numbers (integers). The length of the boat is given in feet (is several feet), the captain has both sons and daughters, he has more years than children, but he is not yet one hundred years old.

	Select Click for Answer
The prime factors of 32,118 are 2, 3, 53, and 101. There are only six ways to decompose it into three factors that are different from 1: 6 × 53 × 101 3 × 101 × 106 3 × 53 × 202 2 × 101 × 159 2 × 53 × 303 2 × 3 × 5,353 Of these possibilities, only the first includes two factors in the range from 4 (the minimum number of children) to 99 (the captain’s maximum age). So the captain has 6 children, he’s 53 years old, and his boat is 101 feet long. From George Polya, The Stanford Mathematics Problem Book, 1974.

Click for Answer

November 17, 2023November 16, 2023 | Puzzles

A Tangle

A problem from the October 1960 issue of Eureka, the journal of the Cambridge University Mathematical Society:

Which of the following knots are knotted and which not?

https://www.archim.org.uk/eureka/archive/index.html — Image: Eureka

	Select Click for Answer
(a) Not knot, (b) Knot, (c) Knot, (d) Not knot.

November 11, 2023November 10, 2023 | Puzzles

“Stock-Breeding”

From John Scott, The Puzzle King, 1899:

“A farmer, being asked what number of animals he kept, answered: ‘They’re all horses but two, all sheep but two, and all pigs but two.’ How many had he?”

	Select Click for Answer
Three. 11/09/2023 UPDATE: There’s another solution: Possibly he has no horses, sheep, or pigs but two llamas (or any other sort of animal). That works too. (Thanks, Gareth and Bob.)

November 8, 2023November 9, 2023 | Puzzles

A Self-Descriptive Crossword Puzzle

From Lee Sallows:

Can you complete the ‘self-descriptive crossword puzzle’ at left below? As in the solution to a similar puzzle seen at right, each of its 13 entries, 6 horizontal, 7 vertical, consists of an English number name folowed by a space followed by a distinct letter. The number preceding each letter describes the total number of occurrences of the letter in the completed puzzle. Hence, in the example, E occurs thirteen times, G only once, and so on, as readers can check. Note that the self-description is complete; every distinct letter is counted.

Though far from easy, the self-descriptive property of the crossword enables its solution to be inferred from its empty grid using reasoning based on orthography only.

	Select Click for Answer
Further information about the construction of such crosswords can be found at https://www.leesallows.com/files/Reflexicons%20NEW(4c).pdf (Thanks, Lee!)

November 7, 2023November 9, 2023 | Puzzles

Snow Manipulation

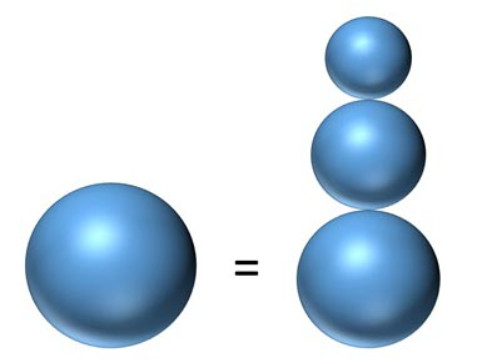
A puzzle by James M., an operations researcher at the National Security Agency:

Frosty the Snowman wants to create a small snowman friend for himself. The new snowman needs a base, torso, and a head, all three of which should be spheres. The torso should be no larger than the base and the head should be no larger than the torso.

For building material, Frosty has a spherical snowball with a 6-inch radius. Since Frosty likes to keep things simple, he also wants the radius of each of the three pieces to be a positive integer. Can Frosty accomplish this?

	Select Click for Answer
Yes! The formula for the volume of a sphere with radius r is $\frac{4}{3}\pi r^{3}$ . Let a, b and c be the radii of the base, torso, and head, respectively, which are integers greater than 0. The problem then amounts to Frosty solving the equation $\displaystyle \frac{4}{3}\pi 6^{3} = \frac{4}{3}\pi a^{3} + \frac{4}{3}\pi b^{3} + \frac{4}{3}\pi c^{3} = \frac{4}{3}\pi \left ( a^{3} + b^{3} + c^{3}\right ).$ By canceling out the factor of $\frac{4}{3}\pi$ from both sides, we’re left with $\displaystyle 216 = a^{3} + b^{3} + c^{3}$ As stated in the problem, a ≥ b ≥ c. The biggest that a can be is 5, so let’s try that first. Subtracting 5³ = 125 from both sides gives us $\displaystyle 91 = b^{3} + c^{3}$ The biggest that b can be is 4, so let’s try that next. Subtracting 4³ = 64 from both sides gives us $\displaystyle 27 = c^{3}$ Frosty is in luck, since 3³ = 27. Thus we have that 6³ = 5³ + 4³ + 3³. Now Frosty can build his new snowman friend to his specifications. In fact, (5, 4, 3) is the only combination of numbers that will work. From NSA’s Puzzle Periodical series.

Click for Answer

November 3, 2023November 2, 2023 | Puzzles

“The Unlucky Hatter”

From The Book of 500 Curious Puzzles, 1859:

A blackleg passing through a town in Ohio, bought a hat for $8 and gave in payment a $50 bill. The hatter called on a merchant near by, who changed the note for him, and the blackleg having received his $42 change went his way. The next day the merchant discovered the note to be a counterfeit, and called upon the hatter, who was compelled forthwith to borrow $50 of another friend to redeem it with; but on turning to search for the blackleg he had left town, so that the note was useless on the hatter’s hands. The question is, what did he lose — was it $50 besides the hat, or was it $50 including the hat?

This is not so much a puzzle as a perplexity. “[I]n almost every case the first impression is, that the hatter lost $50 besides the hat, though it is evident he was paid for the hat, and had he kept the $8 he needed only to have borrowed $42 additional to redeem the note.”

October 27, 2023October 26, 2023 | Puzzles

The Unheard Islander

A puzzle by Edward J. Barbeau, from the February 2007 issue of Crux Mathematicorum:

A certain familiar island is inhabited by knights, who can only speak the truth, and knaves, who can only lie. One day a visitor meets three inhabitants, A, B, and C. The visitor asked, “How many knights are there among you three?”

A gave an answer, which the visitor didn’t hear. When the visitor asked B what A had said, B replied, “A said that there is one knight among us.” At this C said, “Don’t believe B. He is lying.”

What are B and C?

	Select Click for Answer
This solution is by Mandy Rodgers and Josh Trejo. C accuses B of lying, so they can’t both be knights or both knaves. Assume first that B is a knight and C is a knave. That would mean that A really did tell the visitor that there was one knight among the three islanders. But if A’s statement were true then both A and B would be knights, which is a contradiction; and if A’s statement were false then B really would be the only knight, which again is a contradiction. So B can’t be a knight. That means that B is a knave, which makes C a knight. Note that we don’t know whether A is a knight or a knave. It’s possible that he’s a knight and said that the trio includes two knights, which would be true (in this case A/B/C are knight/knave/knight). And it’s possible that he’s a knave and said that all three were knights or all knaves, both of which statements we know are false. These possibilities are both self-consistent, so we can’t say anything about A’s identity, only that B lies and C tells the truth. Obligatory John Finnemore sketch:

Click for Answer

October 25, 2023October 24, 2023 | Puzzles

The Six Submarines

A puzzle by Henry Dudeney:

If five submarines, sunk on the same day, all went down at the same spot where another had previously been sunk, how might they all lie at rest so that every one of the six U-boats should touch every other one? To simplify we will say, place six ordinary wooden matches so that every match shall touch every other match. No bending or breaking allowed.

	Select Click for Answer
It will be seen from the illustration that this puzzle is absurdly easy — when you know how to do it! And yet I have not the slightest doubt that many readers found it a hard nut to crack. It will be seen that every match undoubtedly touches every other match. From Dudeney’s Modern Puzzles and How to Solve Them, 1926. Related: Suppose we’re coloring a map and we decide that no two adjoining regions should have the same color. What’s the smallest number of colors we’ll need to be sure of doing the job? On a flat map the answer is famously four. But what if we extend the question to three dimensions and try to color regions in space? In that case we might need any number of colors, as shown in this “proof without words” by CMG Lee: Image: Wikimedia Commons

Click for Answer

October 24, 2023October 24, 2023 | Puzzles · Science & Math

Poser

From reader Éric Angelini:

What is the smallest number that doesn’t have a 1 and yet has one?

	Select Click for Answer
2,000,008. It doesn’t contain the digit 1, but its English name contains the string ONE (two milliON Eight). (Thanks, Éric.) 10/22/2023 UPDATE: Full credit for the answer none! Thanks to the readers who pointed this out.

October 22, 2023October 22, 2023 | Puzzles

More Self-Description

From reader Ian Duff:

“It is easy to establish that the self-descriptive phrase ‘this phrase contains thirty-five letters’ is the only such one with a correct count. No equivalent is possible in French or German, but in Italian questa frase contiene XX lettere, where XX is a number in word form, again has only one solution.”

What is it?

	Select Click for Answer
The words questa frase contiene lettere contain in total 26 letters, adding venti raises the count to 31, adding trenta raises it to 32, adding quaranta increases it to 34. So venti (or vent for the partial name of 21 or 28) is not feasible, leaving only trenta or quaranta. Considering the number of letters in the single-digit suffixes uno, due, tre, quattro, cinque, sei, sette, otto and nove (and allowing for the dropping of the final letter of trenta and quaranta when naming 31, 38, 41 and 48), only one match is found for the count in the possible range of 30 to 49: The self-descriptive phrase questa frase contiene trentasette lettere does indeed contain 37 letters. (Thanks, Ian.)

Click for Answer

October 17, 2023October 16, 2023 | Language · Puzzles