From Lee Sallows:
Earlier this year, Futility Closet featured a puzzle based upon the well-known 7-segment display. Less well known is the 15-cell display shown in Figure 1, in which each decimal digit appears as a pattern of highlighted cells within a 3×5 rectangle. Call these the small rectangles. Observe also that the digit 1 is represented as the vertical column of 5 cells in the centre of its small rectangle rather than as either of the two alternative columns immediately to left and right, a detail that is important in view of what follows.

Figure 1.
Figure 2 shows a pair of readouts using 15-cell displays each arranged in the form of a (large) 3×5 rectangle that mirrors the smaller rectangles just mentioned. The two readouts describe each other. The top left cell in the right-hand readout contains the number 18. A check will show that the number of highlighted top left cells appearing in the left-hand readout is indeed 18. Take for instance the top left-hand cell in the left-hand readout. It contains the number 17, which employs two digits, 1 and 7. None of the 5 cells forming the digit 1 is in top left position within its small rectangle. But the leftmost cell in digit 7 is indeed in top left position. Proceeding next to the left-hand readout’s top centre cell we find two cells in top left position: one in digit 2 and one in digit 4. The score of top left cells so far is thus 1+2 = 3. Continuing in normal reading order, a list of the left-hand readout numbers followed by their top left cell scores in brackets is as follows: 17 (1), 24 (2), 17(1), 13(1), 9(1), 15(1), 17(1), 25(2), 17(1), 8(1), 9(1), 14(1), 15(1), 24(2), 17(1). The sum of the scores is 18, as predicted.
In the same way, a number occupying position x in either of the readouts will be found to identify the total number of cells occurring in position x within the digits of the other readout. That is, the two readouts are co-descriptive, they describe each other.
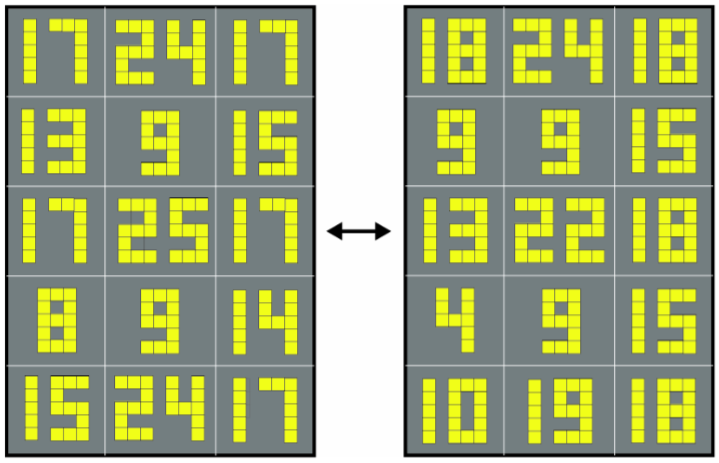
Figure 2.
Recalling now the solution to the earlier mentioned 7-segment display puzzle, some readers may recall that it involved an iterative process that terminated in a loop of length 4. Likewise, the pair of readouts in Figure 2 are the result of a similar process, but now terminating in a loop of length 2. In that case we were counting segments, here we are counting cells. An obvious question thus prompted is: What kind of a readout would result from a loop of length 1? The answer is simple: a description of the readout resulting from a loop of length 1 would be a copy of the same readout. That is, it will be a self-descriptive readout, the description of which is identical to itself. Such a readout does indeed exist. Can the reader find it?
|
SelectClick for Answer |
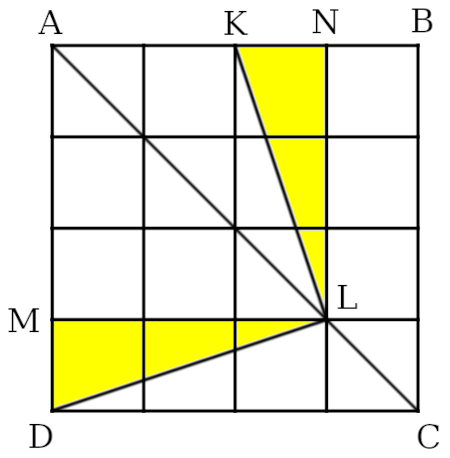
The figure below shows one of two solutions to the puzzle. As the reader can verify, the position of each number in the readout is the position of those yellow cells within their smaller rectangles that the number counts.
Consider now the digit 6 that occurs in the leftmost cell of the fourth row of the readout. If we excise the yellow cell in that same position within the digit it will be turned from a 6 into a 5. Which will still be an accurate count of the yellow cells occupying that position. So changing the 6 into a 5 does not affect the readout’s self-descriptive property, and thus provides us with a genuine, if trivially distinct, second solution.

Figure 3.
(Thanks, Lee!)
|