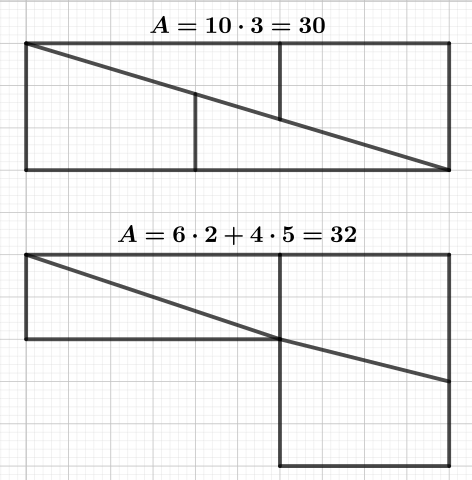
I just ran across this anecdote by Jason Rosenhouse in Notices of the American Mathematical Society. In a middle-school algebra class Rosenhouse’s brother was given this problem:
There are some horses and chickens in a barn, fifty animals in all. Horses have four legs while chickens have two. If there are 130 legs in the barn, then how many horses and how many chickens are there?
The normal solution is straightforward, but Rosenhouse’s brother found an alternative that’s even easier: “You just tell the horses to stand on their hind legs. Now there are fifty animals each with two legs on the ground, accounting for one hundred legs. That means there are thirty legs in the air. Since every horse has two legs in the air, we find that there are fifteen horses, and therefore thirty-five chickens.”
(Jason Rosenhouse, “Book Review: Bicycle or Unicycle?: A Collection of Intriguing Mathematical Puzzles,” Notices of the American Mathematical Society, 67:9 [October 2020], 1382-1385.)